БСЭ БСЭ - Большая Советская Энциклопедия (МЕ)

Ме'о,название части народа мяо, живущей в странах Юго-Восточной Азии — ДРВ, Лаосе, Таиланде и Камбодже.

« Ме'оре-Да'си»(«вторая группа»), общественно-идейное течение в Грузии 19 в. В 1877 выделилось из единого демократического течения т. н. тергдалеулеби (грузинских шестидесятников). К «М.-д.» принадлежали Н. Николадзе, Г. Церетели, С. Месхи, О. Бакрадзе и др., придерживавшиеся по многим вопросам взглядов утопических социалистов и русских революционных демократов. Меоредасовцы с демократических позиций критиковали отрицательные стороны капитализма. Объективно они выражали интересы развивавшейся грузинской буржуазии. Свои взгляды пропагандировали на страницах прогрессивных газет и журналов — «Дроеба» , «Тифлисский вестник», «Обзор», «Моамбе» («Вестник»), «Квали» («Борозда») и др.

Лит.: Ратиани П. К., Грузинские шестидесятники в русском освободительном движении, пер. с груз., Тб., 1968.

Меоти'да(греч. Maiotis, лат. Maeotis, Meotis), название Азовского моря у древних греков и римлян (7 в. до н. э. — 4 в. н. э.), связанное с названием местных племён меотов.

Мео'ты(греч. Maiotai, лат. Maeotae), собирательное название древних племён, обитавших в 1-м тыс. до н. э. на восточном и юго-восточном побережье Азовского моря и по среднему течению Кубани. Название «М.» встречается у античных авторов и в надписях Боспорского царства. Древнегреческий историк и географ Страбон относил к М. синдов, дандариев, досхов и др. М. занимались земледелием и рыболовством. Часть М. по языку была родственна адыгам, часть ираноязычна. В 4—3 вв. до н. э. многие из М. вошли в состав Боспорского государства.

Мепробама'т,лекарственный препарат из группы успокаивающих средств (транквилизаторов); то же, что андаксин.

Ме'рав метрологии, см. в ст. Меры.

Ме'ра мно'жества,математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (D) любого квадрата D полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов D 1, D 2,..., D n,...; нижнюю грань чисел

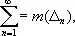
взятую по всевозможным покрытиям множества А , называют верхней (внешней) мерой m *( А ) множества А . Нижняя (внутренняя) мера m * ( А ) множества А определяется как разность

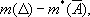
где D — какой-либо квадрат, содержащий множество А , и 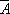— множество всех точек этого квадрата, не содержащихся в А . Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m ( А ) верхней и нижней мер — мерой Лебега множества А . Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область ) , измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.

Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m ( A )D '³ '0; 2) мера суммы

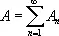
конечной или счётной системы попарно непересекающихся множеств A 1, A 2..., A n... равна сумме их мер:

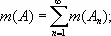
3) при перемещении множества как твёрдого тела его мера не меняется.

Своеобразие понятия «М. м.» можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А , так и точки множества В ; в то же время они резко различаются по мере: m ( А ) = 0, а m ( В ) = 1.

Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.

Развитие ряда отделов современной математики привело к дальнейшим обобщениям — созданию т. н. абстрактной теории меры. При этом М. м. определяют аксиоматически. Пусть U — произвольное множество и 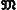— некоторое семейство его подмножеств. Неотрицательную функцию μ( A ), определённую для всех А , входящих в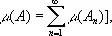

и если, кроме того, система удовлетворяет определённым дополнительным условиям. Множества, входящие в , называют измеримыми (по отношению к мере m). После того как определена мера m, вводят понятие измеримых (по отношению к m) функций и операцию интегрирования.

Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.

Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. — Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.

Ю. В. Прохоров.

Ме'ра пресече'ния, вуголовно-процессуальном праве мера временного ограничения личной свободы обвиняемого. В СССР устанавливается в целях предупреждения попыток скрыться от дознания, следствия или суда, препятствовать установлению истины или продолжать преступную деятельность, а также для обеспечения исполнения приговора. Назначается лицом, производящим дознание, следователем, прокурором и судом при наличии предусмотренных законом оснований. М. п. являются: подписка о невыезде, личное поручительство или поручительство общественных организаций, залог, заключение под стражу (арест) и др. В исключительных случаях М. п. могут применяться в отношении подозреваемого. См. также Предварительное заключение.