БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

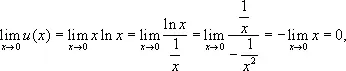
и, следовательно,

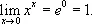
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1, М., 1973.

Неопределённый интегра'л,общее выражение первообразной для подынтегральной функции f ( x ); обозначается

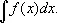
Например,

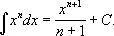
См. Интегральное исчисление .

Неопределённых коэффицие'нтов ме'тод,метод, применяемый в математике для отыскания коэффициентов выражений, вид которых заранее известен. Так, например, на основании теоретических соображений дробь

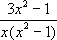
может быть представлена в виде суммы

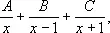
где А, В и С — коэффициенты, подлежащие определению. Чтобы найти их, приравнивают второе выражение первому:

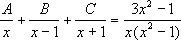
и, освобождаясь от знаменателя и собирая слева члены с одинаковыми степенями х, получают:

( А + В + С ) х 2 + ( В - С ) х - А = 3 x 2- 1.

Так как последнее равенство должно выполняться для всех значений х, то коэффициенты при одинаковых степенях х справа и слева должны быть одинаковыми. Т. о., получаются три уравнения для определения трёх неизвестных коэффициентов: А + В + С = 3, В - С = 0, А = 1, откуда А = В = С = 1. Следовательно,

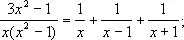
справедливость этого равенства легко проверить непосредственно. Пусть ещё нужно представить дробь

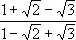
в виде

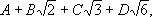
где А, В, С и D — неизвестные рациональные коэффициенты. Приравниваем второе выражение первому

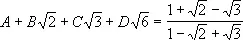
или, освобождаясь от знаменателя, вынося, где можно, рациональные множители из-под знака корней и приводя подобные члены в левой части, получаем:

Но такое равенство возможно лишь в случае, когда равны между собой рациональные слагаемые обеих частей и коэффициенты при одинаковых радикалах. Т. о., получаются четыре уравнения для нахождения неизвестных коэффициентов А, В, С и D: А - 2 B + 3 C = 1, — А + В + 3 D = 1, A + C - 2 D =—1, В - С + D = 0, откуда A = 0, В = — 1/ 2, С = 0, D = 1/ 2, т. е.

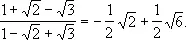
В приведённых примерах успех Н. к. м. зависел от правильного выбора выражений, коэффициенты которых отыскивались. Если бы в последнем примере вместо выражения

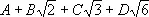
было взято выражение

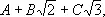
то, рассуждая, как и выше, получили бы для трёх коэффициентов А, В и С четыре уравнения А - 2 В + 3 С = 1 , —A - B = 1, A + C = — 1, В - С = 0, которым нельзя удовлетворить никаким выбором чисел А, В и С .

Особенно важны применения Н. к. м. к задачам, в которых число неизвестных коэффициентов бесконечно. К ним относятся задача деления степных рядов, задача нахождения решения дифференциального уравнения в виде степенного ряда и др. Пусть, например, нужно найти решение дифференциального уравнения у" + ху = 0 такое, что у = 0 и y' = 1 при х = 0. Из теории дифференциальных уравнений следует, что такое решение существует и имеет вид степенного ряда

у = х + c 2x 2+ c 3x 3+ c 4x 4+ c 5x 5+ ×××.

Подставляя это выражение вместо у в правую часть уравнения, а вместо y " — выражение

2 c 2+ 3·2 с 3х + 4·3 с 4х 2 + 5·4с 5х 3+ ×××,

затем, умножая на х и соединяя члены с одинаковыми степенями х, получают

2 c 2+ 3·2 c 3 x + (1 + 4·3 c 4) x 2+ ( c 2+ 5·4 c 5) x 3+ ××× = 0,

откуда при определении неизвестных коэффициентов получается бесконечная система уравнений: 2 c 2= 0; 3·2 с 3= 0; 1 + 4·3 c 4= 0; c 2+ 5·4 c 5= 0;...

Решая последовательно эти уравнения,

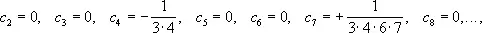
т. е.

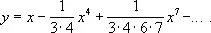
Лит.: Смирнов В. И., Курс высшей математики, т. 1, 23 изд., М., 1974; т. 2, 20 изд., М., 1967; Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.

Неоптоле'м(другое имя — Пирр), в древнегреческой мифологии сын Ахилла и царевны Деидамии, один из главных участников Троянской войны. Вместе с др. воинами проник в чреве деревянного коня в Трою, свирепствовал при её захвате (безжалостно убил на глазах у Гекубы престарелого царя Приама, искавшего спасения у алтаря Зевса).

Неоргани'ческая хи'мия,наука о химических элементах и образуемых ими простых и сложных веществах (кроме соединений углерода, составляющих, за немногими исключениями, предмет органической химии ) . Н. х. — важнейшая область химии— науки о превращениях вещества, сопровождающихся изменениями его состава, свойств и (или) строения. Н. х. теснейшим образом связана, помимо органической химии, с др. разделами химии — аналитической химией, коллоидной химией, кристаллохимией, физической химией, термодинамикой химической, электрохимией, радиохимией, химической физикой; на стыке неорганической и органической химии лежит химия металлоорганических соединений и элементоорганических соединений. Н. х. ближайшим образом соприкасается с геолого-минералогическими науками, особенно с геохимией и минералогией, а также с техническими науками — химической технологией (её неорганической частью), металлургией— и агрохимией. В Н. х. постоянно применяются теоретические представления и экспериментальные методы физики.