БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

Лит.: Зограф Г. А., Языки Индии, Пакистана, Цейлона и Непала, М., 1960; Королев Н. И., Язык Непала, М., 1965 (есть лит.): Непальско-русский словарь, М., 1968, с. 1211—1328; Srivastaya Dayanand, Nepali language, its history and development, Calcutta, 1962; Turner R. L., A comparative and etymological dictionary of the Nepali language, N. Y., 1966.

Н. И. Королев.

Непа'льцы,непали,

1) название всех граждан Непала.

2) Самоназвание, распространившееся среди народов Непала, вошедших в конфедерацию гуркхов и постепенно консолидировавшихся в единый народ, ныне составляющий около половины населения страны. Говорят на непальском языке. (Об истории, хозяйстве и культуре Н. см. в ст. Непал. )

Непараметри'ческие ме'тодыв математической статистике, методы непосредственной оценки теоретического распределения вероятностей и тех или иных его общих свойств (симметрии и т.п.) по результатам наблюдений. Название Н. м. подчёркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений ) , и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Разработка Н. м. является в значительной степени заслугой советских учёных.

В качестве примера Н. м. можно привести найденный А. Н. Колмогоровым способ проверки согласованности теоретических и эмпирических распределений (так называемый критерий Колмогорова). Пусть результаты n независимых наблюдений некоторой величины имеют функцию распределения F ( x ) и пусть F n ( x ) обозначает эмпирическую функцию распределения (см. Вариационный ряд ) , построенную по этим n наблюдениям, a D n— наибольшее по абсолютной величине значение разности F n ( x ) — F ( x ) . Случайная величина

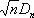
имеет в случае непрерывности F ( x ) функцию распределения K n (l) , не зависящую от F ( x ) и стремящуюся при безграничном возрастании n к пределу

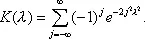
Отсюда при достаточно больших n, для вероятности p n, l . Неравенства

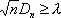
получается приближённое выражение

p n, l» 1 - К (l). (*)

Функция К (l) табулирована. Её значения для некоторых А приведены в табл.

Таблица функции К (l)

Равенство (*) следующим образом используется для проверки гипотезы о том, что наблюдаемая случайная величина имеет функцию распределения F ( x ) : сначала по результатам наблюдений находят значение величины D n, а затем по формуле (*) вычисляют вероятность получения отклонения F n от F, большего или равного наблюдённому. Если указанная вероятность достаточно мала, то в соответствии с общими принципами проверки статистических гипотез (см. Статистическая проверка гипотез ) проверяемую гипотезу отвергают. В противном случае считают, что результаты опыта не противоречат проверяемой гипотезе. Аналогично проверяется гипотеза о том, получены ли две независимые выборки, объёма n 1 и n 2 соответственно, из одной и той же генеральной совокупности с непрерывным законом распределения. При этом вместо формулы (*) пользуются тем, что вероятность неравенства

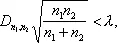
как это было установлено Н. В. Смирновым, имеет пределом К (l) , здесь D n1, n2 есть наибольшее по абсолютной величине значение разности F n1 ( х ) — F n2 ( х ) .

Другим примером Н. м. могут служить методы проверки гипотезы о том, что теоретическое распределение принадлежит к семейству нормальных распределений. Отметим здесь лишь один из этих методов — так называемый метод выпрямленной диаграммы. Этот метод основывается на следующем замечании. Если случайная величина Х имеет нормальное распределение с параметрами a и s, то

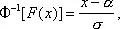
где Ф -1— функция, обратная нормальной:

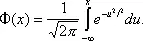
Т. о., график функции у = Ф -1 [ F ( x )] будет в этом случае прямой линией, а график функции у = Ф -1 [ F n (x)] — ломаной линией, близкой к этой прямой (см. рис. ). Степень близости и служит критерием для проверки гипотезы нормальности распределения F ( x ) .

Лит.: Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; Большее Л. Н., Смирнов Н. В., Таблицы математической статистики, М., 1968.

Ю. В. Прохоров.

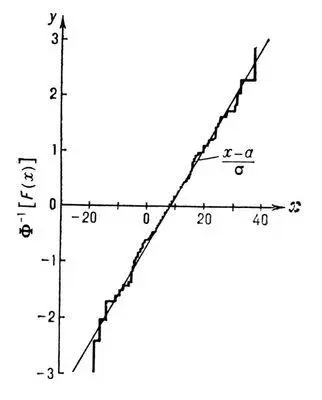
Рис. к ст. Непараметрические методы.

Непарнокопы'тные,непарнопалые (Perissodactyla), отряд млекопитающих. Крупные, реже средней величины животные. Число пальцев на передних конечностях 1, 3 или 4, на задних — 1 или 3. Третий палец развит сильнее других и несёт основную тяжесть тела животного. Конечные фаланги пальцев у Н. одеты копытами. Коренные зубы с поперечными и продольными гребнями (складками) на жевательной поверхности, приспособлены к перетиранию жёсткой растительной пищи. Лицевой отдел черепа длинный. Ключицы отсутствуют. В отличие от парнокопытных, на бедренной кости имеется третий вертел. Растительноядны. Желудок простой, однокамерный. Слепая и ободочная кишки длинные, объёмистые, имеют большое число выпячиваний — карманов, что облегчает переваривание грубой пищи. Матка двурогая, плацента диффузная. 1 пара молочных желёз, расположенных в паховой области. Приносят по 1 детёнышу. Распространены Н. в Африке, Азии и Южной Америке, а в домашнем состоянии — на всех материках; в Южной Европе в диком состоянии Н. обитали до конца 19 в. В современной фауне Н. представлены 3 семействами: лошадиные, носороги и тапиры.

Лит.: Соколов И. И., Копытные звери, М. — Л., 1959 (Фауна СССР. Млекопитающие, т. 1, в. 3); Млекопитающие Советского Союза, т. 1, М., 1961.

И. И. Соколов.