БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

Понятию Н. ф. противопоставляется понятие разрывной функции. Одна и та же функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробная часть числа х [её принято обозначать через ( х )] , например

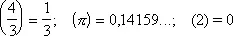
является функцией разрывной при любом целом значении и непрерывной при всех других значениях ( рис. 1 ), причём в целочисленных точках она непрерывна справа.

Простейшими функциями переменного х, непрерывными при всяком значении x , являются многочлены, синус ( у = sin x), косинус ( у = cos x), показательная функция ( у = a x , где а — положительное число). Сумма, разность и произведение Н. ф. снова дают Н. ф. Частное двух Н. ф. также есть Н. ф., за исключением тех значений х, для которых знаменатель обращается в нуль (так как в таких точках рассматриваемое частное не определено). Например,

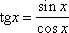
есть Н. ф. для всех значений х, кроме нечётных кратных p/2, при которых cos х обращается в нуль.

Н. ф. обладают многими важными свойствами, которыми и объясняется огромное значение этих функций в математике и её приложениях. Одно из важнейших свойств выражается следующей теоремой: для всякой функции, непрерывной на отрезке [ а, b ] можно найти многочлен, значения которого отличаются на этом отрезке от значений функции менее чем на произвольно малое, наперёд заданное число (теорема о приближении Н. ф. многочленами). Справедлива также и обратная теорема: всякая функция, которую на некотором отрезке можно с произвольной степенью точности заменить многочленом, непрерывна на этом отрезке.

Функция, непрерывная на отрезке, ограничена на нём и достигает на этом отрезке наибольшего и наименьшего значения (см. Наибольшее и наименьшее значения функций ) . Кроме того, она принимает на этом отрезке все значения, лежащие между её наименьшим и наибольшим значениями. Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности. Всякая функция, непрерывная на некотором отрезке, интегрируема на нём, т. е. является производной другой Н. ф. Однако не всякая Н. ф. сама имеет производную. Геометрически это означает, что график Н. ф. не обязательно обладает в каждой точке определённым направлением (касательной); это может произойти, например, потому, что график имеет угловую точку ( рис.2 , функция у = | x |), или потому, что он совершает в любой близости точки О бесконечно много колебаний между двумя пересекающимися прямыми ( рис. 3 , функция

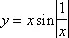
при х ¹ 0 и y = 0 при x = 0).

Существуют Н. ф., не имеющие производной ни в одной точке (первый пример такого рода был найден Б. Больцано ) . Представление о графике подобной функции даёт рис. 4 , где изображены первые этапы построения, состоящего в неограниченно продолжающейся замене средней трети каждого прямолинейного отрезка двузвенными ломаными; соотношения длин подбираются так, чтобы в пределе получить Н. ф.

Функция F ( x , у, z,... ) нескольких переменных, определённая в некоторой окрестности точки ( x 0, y 0, z 0 ,...), называется непрерывной в этой точке, если для любого e > 0 можно указать такое d > О, что при одновременном выполнении неравенств: | x — x 0 | < d, | у — у 0 | < d, | z — z 0 | < d,... выполняется также и неравенство:

I F ( x , у, z ,...) — F ( x 0 , y 0, z 0,... )| < e.

Такая функция будет непрерывной по отношению к каждому аргументу в отдельности (если остальным аргументам приданы определённые числовые значения). Обратное, однако, неверно: функция F ( x :, у, z, ...), непрерывная по каждому аргументу в отдельности, может и не быть Н. ф. этих аргументов. Простейший пример этого даёт функция F ( x , у ) , равная xy/ ( x 2 + y 2 ) , если x 2 + y 2 ¹ 0 , и равная 0 при x = у = 0. Она непрерывна по x при любом фиксированном значении y по y — при любом фиксированном значении х. В частности, она непрерывна по x при у = 0 и по y при x = 0. Если же положить, например, у = х ¹ 0, то значение функции будет оставаться равным x 2/ ( x 2 + y 2 ) = 1/ 2, т. е. нельзя будет указать такого числа d > 0, чтобы при одновременном выполнении неравенств | х | < d, | у | < d выполнялось неравенство | ху/ ( х 2+ y 2 )| < e . На Н. ф. нескольких переменных распространяются все основные теоремы, относящиеся к Н. ф. одного переменного.

Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970.

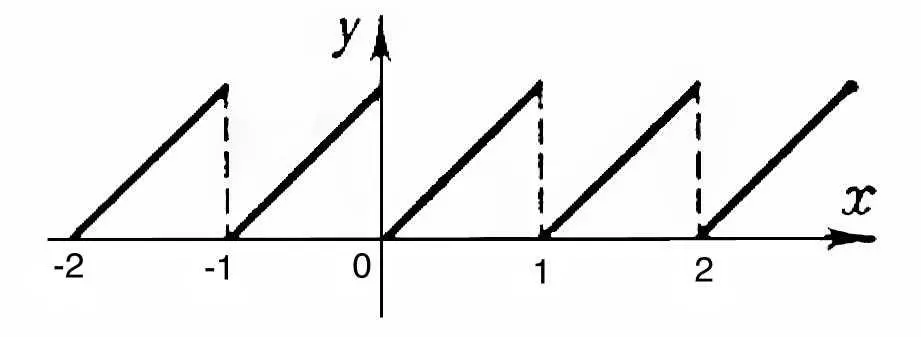
Рис. 1 к ст. Непрерывная функция.

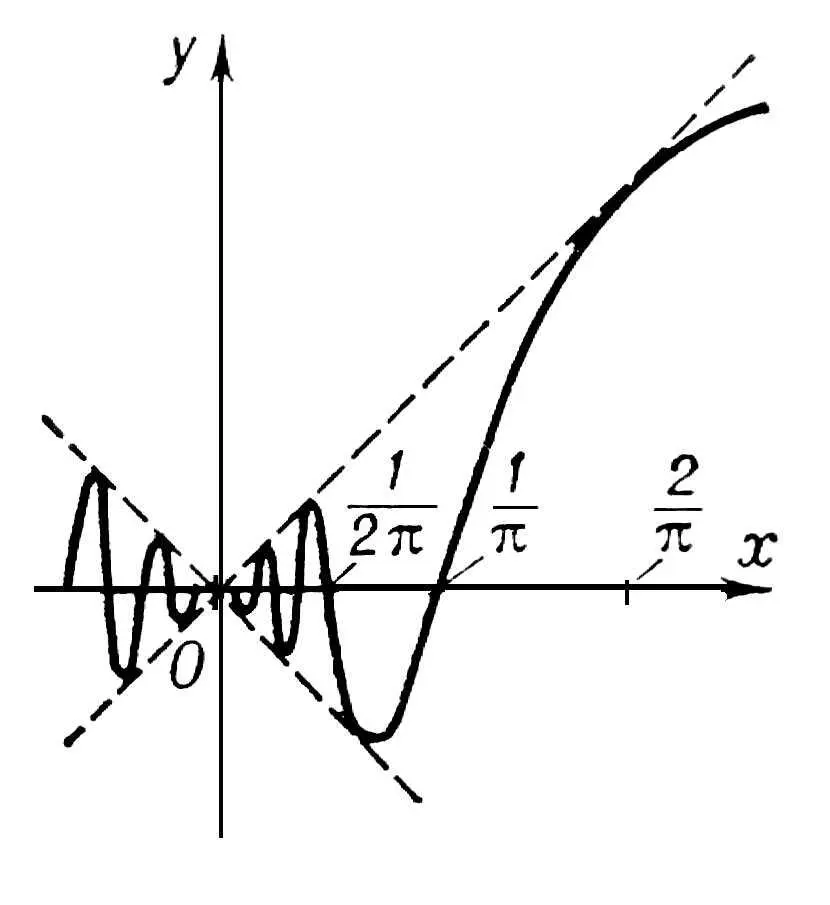
Рис. 3 к ст. Непрерывная функция.

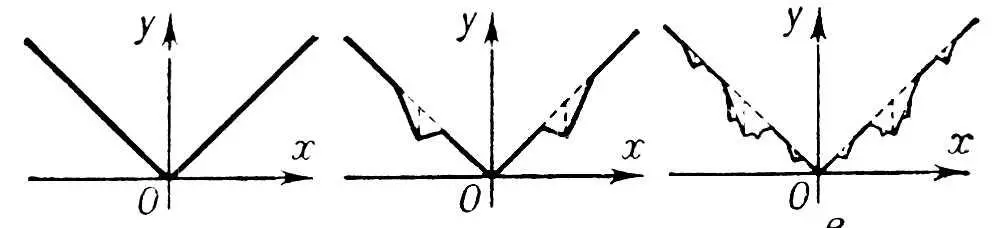
Рис. 4 к ст. Непрерывная функция.

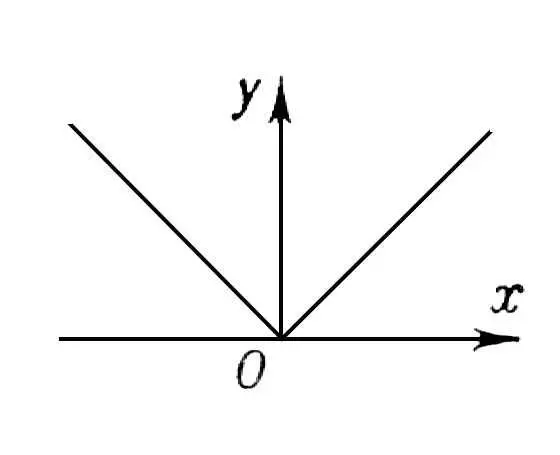
Рис. 2 к ст. Непрерывная функция.

Непреры'вное литьёметаллов и сплавов, процесс получения слитков и заготовок, основанный на равномерном перемещении металла относительно зон заливки и кристаллизации. При этом литейная форма может быть неподвижной или закономерно перемещаться (возвратно-поступательное движение с небольшой амплитудой, вращение, движение по замкнутой кривой ограниченной длины).

Н. л. металлов и сплавов в СССР и за рубежом начали применять в промышленности в 1930-х гг.; широкое распространение оно нашло в середине 40-х гг. Н. л. теоретически позволяет получать отливки сколь угодно большой длины; практически длина отливок определяется возможностями литейного производства, требованиями обрабатывающих цехов и организационно-экономическими соображениями. Получение отливок ограниченной длины методом Н. л. иногда неправильно называют полунепрерывным литьём. Равномерные скорости подачи, жидкого металла, его кристаллизации и удаления готовой отливки при Н. л. обеспечивают постоянство состава, строения и свойств металла по всей длине отливки. Путём усиленного отвода тепла (благодаря непосредственному охлаждению металла водой) можно повысить скорость кристаллизации и при правильно выбранной скорости литья создать направленную кристаллизацию, в основном вдоль оси отливки, что обеспечивает получение плотных слитков или заготовок с тонким внутренним строением зерна и равномерным химическим составом. Помимо того, Н. л. по сравнению со штучным литьём, сокращает количество отходов и потерь металла, затраты рабочей силы, литейной оснастки и инструмента.