БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

Соч.: Твори. [Вступ. ст. О. I. Бiлецького], т. 1—4, К., 1956; Зiбрання творiв, [Вступ. ст. Н. Є. Крутiковой], т. 1—8, К., 1965—67; в рус. пер. — Избр. произведения, т. 1—2, М., 1956.

Лит.: Франко I., Лiтература, iï завдання i найважнiшi цiхи, Твори, т. 16, К., 1955; его же, «Микола Джеря», повiсть Iвана Нечуя, там же, т. 17, К., 1955; Крутiкова Н. Є., Творчiсть I. С. Нечуя-Левицького. [Статтi та матерiали], К., 1961; Походзiло М. У., Iван Нечуй-Левицький, К., 1960.

С. П. Князева.

И. С. Нечуй-Левицкий. «Микола Джеря» (Киев, 1959). Илл. В. В. Полтавца.

И. С. Нечуй-Левицкий.

Неша'вские стату'ты 1454,Нешавские привилеи, привилегии, полученные шляхтой от польского короля Казимира IV под г. Нешава (Nieszawa); были выданы в отдельности для Малой Польши, Великой Польши, земель Серадзской, Хелминьской, Саноцкой и Перемышльской (в основу легли привилегии, данные великопольской шляхте в сентябре 1454 в лагере под Церквицей). Были получены в разгар войны Польши с Тевтонским орденом за поддержку, которую шляхта оказала королю в войне и в его борьбе с магнатами. Отменяли исключительное право магнатов замещать высшие государственные должности, регулировали судопроизводство и местное управление (находившиеся в руках магнатов) в пользу шляхты. Одновременно Н. с. означали и серьёзное ограничение королевской власти. Издание законов, решение вопросов войны и мира могли, согласно Н. с., осуществляться только с согласия шляхетских сеймиков; шляхта освобождалась от суда королевских чиновников (за исключением особых случаев). Н. с. частично ограничивали права городов (в малопольской редакции был пункт, распространявший юрисдикцию шляхетского суда на города). Явились важной вехой в формировании польской шляхетской «республики».

Лит.: Historia państwa i prawa Polski, 2 wyd., t. 1, Warsz., 1965.

Нешта'тные рабо'тники,см. Работники нештатные.

Не'я,город (до 1958 — посёлок) областного подчинения, центр Нейского района Костромской области РСФСР. Расположен на правом берегу р. Нея (приток р. Унжа). Ж.-д. станция на линии Буй — Котельнич. Крупный центр лесопильно-деревообрабатывающей промышленности (лесозавод, завод «Музлесдрев», леспромхоз). Авторемонтный, маслосыродельный заводы, льнозавод, швейная фабрика.

Не'я,река в Костромской области РСФСР, правый приток р. Унжа (бассейн Волги). Длина 253 км, площадь бассейна 6060 км 2. Берёт начало на Галичской возвышенности. Питание смешанное, с преобладанием снегового. Средний расход воды в 38 км от устья 45,5 м 3/сек. Замерзает в ноябре, вскрывается в апреле. Сплавная. На реке — г. Нея.

Нея'вные фу'нкции,функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение

x 2 + y 2- 1 = 0

задаёт Н. ф.

y = у ( х ) ,

соотношения

x = rcosjsinJ, y = rsinjsinJ , z = rcosJ

задают Н. ф.:

r = r( x , у, z ), j = j( x , y, z ) , J = J( х, у, z ) .

В простейших случаях соотношения, задающие Н. ф., могут быть разрешены в классе элементарных функций, т. е. удаётся найти элементарные функции, удовлетворяющие этим соотношениям. Так, в первом из приведённых выше примеров имеем:

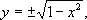
а во втором:

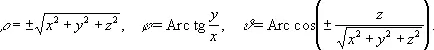
Вообще же таких элементарных функций найти не удаётся. Н. ф. могут быть как однозначными, так и многозначными. Не всякое соотношение (или система соотношений) между переменными задаёт Н. ф. Так, если ограничиваться лишь действительными значениями переменных, то соотношение x 2 + y 2 + 1 = 0 не задаёт Н. ф., так как не удовлетворяется ни одной парой действительных значений х и у; соотношение же e xy = 0 вообще не удовлетворяется ни одной парой действительных или комплексных значений х и у. Теорема существования Н. ф. в её простейшей формулировке утверждает, что если функция F ( x, y ) обращается в нуль при паре значений х = x 0, у = y 0 [ F ( x 0, y 0 ) ¹ 0] и дифференцируема в окрестности точки ( x 0, y 0 ) , причём F’ x ( х, у ) и F’ y ( х, у ) непрерывны в этой окрестности и F’ y ( x 0, y 0 ) ¹ 0, то в достаточно малой окрестности точки x 0существует одна и только одна однозначная непрерывная функция у = у ( х ) , удовлетворяющая соотношению F ( x, y ) = 0 и обращающаяся в y 0при x = x 0; при этом y '( x ) = — F’ x ( x, y ) /F’ y ( x, у ) .

Для приближённого вычисления значений Н. ф. вблизи точки x 0 , где её значение y 0уже известно, широко применяются степенные ряды. Так, если F ( x, у ) — аналитическая функция [т. е. может быть разложена в окрестности точки ( x 0, y 0) в сходящийся двойной степенной ряд] и F’ y ( x 0, y 0) ¹ 0, то Н. ф., заданная соотношением F ( x, y ) = 0, может быть получена в виде степенного ряда

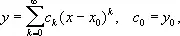
сходящегося в некоторой окрестности точки х = х 0. Коэффициенты c k , k = 1, 2,..., могут быть найдены либо подстановкой этого ряда в соотношение F ( x , у ) = 0, либо последовательным дифференцированием этого соотношения по х. Например, если Н. ф. задана соотношением

y 5 + xy - 1 = 0, x 0= 0, y 0= 1,

то

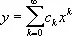
и

откуда

c 0= 1, c 1= — 1/ 5 c 0 -3, c 2= —2 c 1 2 c 0 -1— 1/ 5 c 1 c 0 -4= — 1/ 25и т.д.

Если соотношение F ( x, у ) = 0 может быть представлено в виде у = а + х j( у ) , где j( y ) — аналитическая функция, то Н. ф. у = у ( х ) , заданная этим соотношением и принимающая значение а при х = 0, разлагается в ряд Лагранжа