БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

Аналогично описанной выше «дедуктивной» Н. можно говорить о Н. «выразительной», называя понятие (термин) независимым от данной системы понятий (терминов), если оно не может быть определено лишь с их помощью (опять-таки, как и выше, здесь предполагается фиксация некоторой совокупности правил определения, относительно которых можно ставить проблему Н.). Термин «Н.» (в обоих упомянутых смыслах) применяется, наконец, и к совокупностям предложений (формул) или понятий (терминов): совокупность называется независимой (а также неизбыточной, или минимальной), если каждый из её членов независим от остальных в определённом выше смысле. Ряд важнейших результатов о Н. получен в аксиоматической теории множеств и в математической логике.

Лит. см. при ст. Аксиоматический метод.

Ю. А. Гастев.

Незави'симостьв теории вероятностей, одно из важнейших понятий этой теории. В качестве примера можно привести определение Н. двух случайных событий. Пусть А и В — два случайных события, а Р ( А ) и Р ( В ) — их вероятности. Условную вероятность Р ( В|А ) события В при условии осуществления события А определяют формулой:

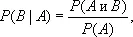
где Р ( А и В ) — вероятность совместного осуществления событий А и В. Событие В называется независимым от события А, если

Р ( В|А ) = Р ( В ). (*)

Равенство (*) может быть записано в виде, симметричном относительно А и В:

Р ( А и В ) = Р ( А ) Р ( В ),

откуда видно, что если событие В не зависит от А, то и А не зависит от В. Т. о., можно говорить просто о Н. двух событий. Конкретный смысл данного определения Н. можно пояснить следующим образом. Известно, что вероятность события находит своё выражение в частоте его появления. Поэтому если производится большое число N испытаний, то между частотой появления события В во всех N испытаниях и частотой его появления в тех испытаниях, в которых наступает событие, должно иметь место приближённое равенство. Н. событий указывает, т. о., либо на отсутствие связи между наступлением этих событий, либо на несущественный характер этой связи. Так, событие, заключающееся в том, что наудачу выбранное лицо имеет фамилию, начинающуюся, например, с буквы «А», и событие, заключающееся в том, что этому лицу достанется выигрыш в очередном тираже лотереи, — независимы.

При определении Н. нескольких (более двух) событий различают попарную и взаимную Н. События A 1 , A 2 , ..., A nназываются попарно независимыми, если каждые два из них независимы в смысле данного выше определения, и взаимно независимыми, если вероятность наступления любого из них не зависит от наступления какой угодно комбинации остальных.

Понятие «Н.» распространяется и на случайные величины . Случайные величины Х и Y называются независимыми, если для любых двух интервалов D 1и D 2события, заключающиеся в том, что значение Х принадлежит D 1, а значение Y — интервалу D 2, независимы. На гипотезе Н. тех или иных событий и случайных величин основаны важнейшие схемы теории вероятностей (см., например, Предельные теоремы теории вероятностей). О способах проверки гипотезы Н. каких-либо событий см. Статистическая проверка гипотез .

Лит.: Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., М., 1964.

Незави'симость су'дей,один из демократических конституционных принципов социалистического правосудия, означающий, что при вынесении решения (приговора, определения, постановления) судьи не связаны никакими соображениями, посторонними правосудию, и обязаны руководствоваться только законом в соответствии с их социалистическим правосознанием (см., например, Конституция СССР, ст. 112).

Организационное построение судебной системы социалистических государств исключает какое-либо влияние со стороны любого вышестоящего (судебного или иного) органа на существо решений или приговоров, выносимых судом по конкретным делам. В целях обеспечения организационной независимости суда законодательство социалистических государств предусматривает целый ряд гарантий, в том числе выборность судей и народных заседателей во всех звеньях судебной системы, право досрочного отзыва избирателями судей, не оправдавших их доверия, особый порядок судебной и дисциплинарной ответственности судей. Н. с. обеспечивается также правовыми гарантиями: непосредственность, непрерывность и устность судебного разбирательства , право отвода судьи, тайна совещательной комнаты , и др.

При вынесении приговора или решения члены данного состава суда независимы друг от друга: это обеспечивается равенством прав всех членов суда (каждый судья может заявить своё особое мнение ).

В буржуазных государствах положение суда в механизме государства теоретически базируется на принципе разделения властей (см. «Разделение властей» ), согласно которому в государстве якобы существуют три самостоятельные и независимые друг от друга власти: законодательная, исполнительная и судебная. Однако на деле в большинстве буржуазных государств судьи назначаются главой государства, они, как правило, несменяемы, что уже само по себе характеризует подчинённость буржуазного суда и самих судей интересам господствующих классов, определяет их зависимость от высших органов власти.

Незако'нная охо'та,по советскому уголовному праву охота без надлежащего разрешения в запрещенных местах либо в запрещенные сроки, запрещенными орудиями и способами. Н. о.

— вид браконьерства , к которому относятся также незаконное занятие рыбным и др. водными добывающими промыслами, незаконный промысел котиков и бобров. Уголовная ответственность за Н. о. наступает, как правило, после применения мер административного воздействия за такое же нарушение. Независимо от административного взыскания считается уголовным преступлением охота на зверей и птиц, добыча которых полностью запрещена.

Незараще'ние нёба,врождённый порок развития человека, при котором в результате образования расщелины между правой и левой половинами твёрдого нёба нарушаются акты питания, дыхания и речи. Составляет до 30% всех пороков развития; часто встречается совместно с заячьей губой . Возникновение Н. и. связано с нарушением хода развития зародыша в периоде 6—12 нед, когда происходит формирование нёба. На развитие Н. н. оказывают влияние неблагоприятные внешние условия, физические и психические травмы матери, недостаточное питание, перенесённые во время беременности заболевания, токсоплазмоз. Влияние наследственности не доказано. Надёжный способ устранения Н. н. и связанных с ним функциональных расстройств — радикальная пластическая операция в сочетании с ортопедическим и логопедическим пред- и послеоперационным лечением. Профилактика: рациональный режим труда и быта беременной, полноценное питание, предохранение от инфекционных заболеваний.