БСЭ БСЭ - Большая Советская Энциклопедия (НЕ)

Описанное явление, называется генерацией оптических гармоник, имеет много общего с широко известным умножением частоты в нелинейных элементах радиоустройств. Вместе с тем есть и существенное различие: в оптике эти эффекты являются результатом взаимодействия не колебаний, а волн. В сильном световом поле, согласно (2), каждый атомный осциллятор переизлучает не только на частоте падающей волны, но и на её гармониках. Однако так как свет распространяется в среде, размеры L которой существенно превышают длину волны l (для видимого света l~ 10 -4 см ) , суммарный эффект генерации гармоник на выходе зависит от фазовых соотношений между основной волной и гармониками внутри среды; возникает своеобразная интерференция, способная либо усилить, либо ослабить эффект. Оказалось, что взаимодействие двух волн, различающихся частотами, например w и 2w, максимально, а, следовательно, максимальна и перекачка энергии от основной волны к гармоникам, если их фазовые скорости равны (условие фазового синхронизма). К условиям фазового синхронизма можно прийти и из квантовых соображений, они соответствуют закону сохранения импульса при слиянии или распаде фотонов. Для трёх волн условия синхронизма: k 3 = k 1 + k 2, где k 1 , k 2 и k 3— импульсы фотонов (в единицах Планка постоянной ) .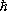

Условия синхронизма основной волны и гармоник в реальной диспергирующей среде на первый взгляд кажутся неосуществимыми. Равенство фазовых скоростей волн на разных частотах имеет место лишь в среде без дисперсии. Однако оказалось, что отсутствие дисперсии можно имитировать, используя взаимодействие волн разной поляризации в анизотропной среде ( рис. 1 ). Этот метод резко повысил эффективность нелинейных волновых взаимодействий. Если в 1961 кпд оптических удвоителей частоты составлял ~10 -10—10 -12 , то в 1963 он достиг значения 0,2—0,3, а к 1973 приблизился к 0,8.

Оптические умножители частоты позволили существенно расширить область применения лазеров. Эффект генерации оптических гармоник широко используется для преобразования излучения длинноволновых лазеров в излучение коротковолновых диапазонов. Промышленность многих стран выпускает оптические умножители частоты на неодимовом стекле или на алюмоиттриевом гранате с примесью неодима (l = 1,06 мкм ) , позволяющие получить мощное когерентное излучение на волнах l = 0,53 мкм (2-я гармоника), l = 0,35 мкм (3-я гармоника) и l = 0,26 мкм (4-я гармоника). Для этой цели были подобраны кристаллы, обладающие высокой нелинейностью (большими значениями c) и позволяющие удовлетворить условиям фазового синхронизма. Иллюстрациями современных возможностей в этой области являются генератор 5-й оптической гармоники ( рис. 2 ) и получение 9-й гармоники излучения неодимового лазера (l 9= 1189 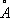). В 1972 было экспериментально осуществлено умножение частоты в области вакуумного ультрафиолета; в качестве нелинейной среды здесь использовались некоторые газы и пары металлов.

Самофокусировка света. Самовоздействия.При достаточно большой (но вполне умеренной для современной лазерной техники) мощности светового пучка, превышающей некоторое критическое значение Р кр , в среде вместо обычной дифракционной расходимости первоначально параллельного пучка наблюдается его самосжатие ( рис. 3 ). Величина Р кр различна для разных сред; для ряда органических жидкостей Р кр ~ 10—50 квт, в некоторых кристаллах и оптических стеклах Р кр не превышает нескольких вт.

Иногда, например, при распространении излучения мощных импульсных лазеров в жидкостях, это самосжатие носит характер «схлопывания» пучка, которое сопровождается настолько быстрым нарастанием светового поля, что это может вызвать световой пробой (см. Лазерное излучение ) , фазовые переходы и др. изменения состояния вещества. В др. случаях, например при распространении излучения газовых лазеров непрерывного действия в стеклах, нарастание поля также заметно, хотя и не является столь быстрым. Самосжатие в некотором смысле похоже на фокусировку пучка обычной линзой. Однако существенные различия наблюдаются за фокальной точкой; самосфокусированный пучок может образовывать квазистационарные нити («волноводное» распространение), последовательность фокальных точек и т.п.

Явление самофокусировки обусловлено тем, что в сильном световом поле изменяется показатель преломления среды (в опыте, изображенном на рис. 3 , это происходит за счёт нагрева стекла лазерным излучением). Если знак изменения показателя преломления таков, что в области, занятой пучком, он возрастает, эта область становится оптически более плотной, и периферийные лучи отклоняются к центру пучка. На рис. 2 изображены фазовые фронты и ход лучей в ограниченном пучке, распространяющемся в среде, с показателем преломления: n = n 0 + n 2E 2, где n 0— постоянная составляющая, не зависящая от Е, n 2> 0. Поскольку фазовая скорость света v = c/n = с/ ( n 0 + n 2E 2 ) , то фазовые фронты изгибаются (поле Е на оси больше, чем на периферии) и лучи отклоняются к оси пучка. Такая нелинейная рефракция может быть столь существенной (её «сила» нарастает вместе с концентрацией поля), что практически полностью подавляет дифракционные эффекты.

Обратный эффект — самодефокусировка — возникает, если среда в области, занятой световым пучком, из-за зависимости показателя преломления от интенсивности становится оптически менее плотной ( n 2 < 0). В этом случае мощный лазерный пучок расходится гораздо быстрее, чем пучок малой интенсивности. Нелинейные волновые явления типа самофокусировки и самодефокусировки, в которых средние частота и волновое число k = w n / c = 2p/l почти не изменяются, называются самовоздействием волн. Наряду с самовоздействием волн, модулированных в пространстве, в Н. о. изучается также самовоздействие волн, модулированных во времени.

Распространение светового импульса в среде с показателем преломления вида n = n 0 + n 2E 2 сопровождается искажением его формы и фазовой модуляцией. В результате возникает сильное уширение спектра лазерного импульса. Ширина спектра излучения на выходе из среды в сотни и тысячи раз превышает ширину спектра на входе.

Эффекты самовоздействия определяют основные черты поведения мощных световых пучков в большинстве сред, включая и активные среды самих лазеров. В частности, лавинное нарастание напряженности светового поля при самофокусировке вызывает во многих случаях оптический пробой среды ( рис. 3 ).