БСЭ БСЭ - Большая Советская Энциклопедия (ОБ)

Аналитически О. может быть выражен с помощью кратных интегралов. Пусть тело К ( рис. 1 ) ограничено цилиндрической поверхностью с параллельными оси Oz образующими, квадрируемой областью М плоскости Оху и поверхностью z = f (x , у) , которую любая параллель к образующей цилиндра пересекает в одной и только в одной точке. Объём такого тела может быть вычислен с помощью двойного интеграла

.

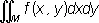О. тела, ограниченного замкнутой поверхностью, которая встречается с параллелью к оси Oz не более чем в двух точках, может быть вычислен как разность О. двух тел, подобных предшествующему. О. тела может быть выражен в виде тройного интеграла

,

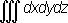где интегрирование распространяется на часть пространства, занятую телом. Иногда удобно вычислять О. тел через его поперечные сечения. Пусть тело ( рис.2 ), содержащееся между плоскостями z = а и z = b ( b > а ), рассекается плоскостями, перпендикулярными оси Oz . Если все сечения тела квадрируемы и площадь сечения S — непрерывная функция от z , то О. тела может быть выражен простым интегралом

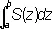. (1)

Исторически происходило так, что задолго до создания интегрального исчисления операция интегрирования фактически применялась (в различных геометрических формах) к вычислению О. простейших тел (пирамиды, шара, некоторых тел вращения), чем и была подготовлена почва для оформления этого исчисления в 17—18 вв. В частности, формулу (1) содержал в зародыше т. н. Кавальери принцип , сохраняющий своё значение для школьного преподавания. В элементарном преподавании полезной оказывается также Симпсона формула , соответствующая тому случаю, когда в (1) функция S (z) является многочленом не выше 3-й степени.

Об обобщениях понятия «О.» см. в ст. Мера множества .

Лит.: Кудрявцев Л. Д., Математический анализ, т. 1—2, М., 1970; Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960.

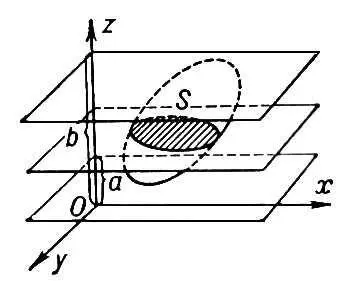
Рис. 2 к ст. Объём.

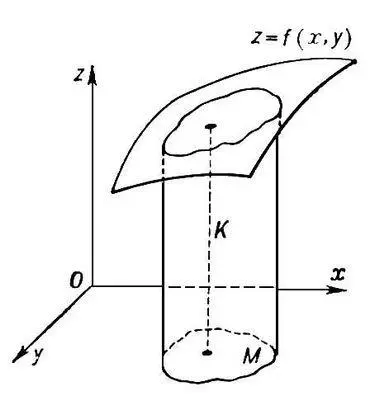
Рис. 1 к ст. Объём.

Объём уде'льныйвещества, физическая величина, определяемая отношением объёма V тела к его массе m . О. у. v однородного вещества определяется по формуле v = V/m . О. у. — величина, обратная плотности . Единицами О. у. служат: 1 м 3/кг в Международной системе единиц и 1 см 3/г в СГС системе единиц . 1 м 3/кг = 10 3 см 3/г .

Объёмная вя'зкость, вторая вязкость, свойство среды (жидкой или газообразной), характеризующее необратимое превращение в ней механической энергии в теплоту, происходящее при объёмных деформациях. О. в. проявляется, например, при распространении звуковых и особенно ультразвуковых волн в жидкостях и газах. Величина коэффициента О. в. h' так же, как и коэффициент сдвиговой вязкости h, определяет величину поглощения звука .

Если при распространении звука равновесное состояние среды практически не нарушается, что справедливо, когда характерное время установления равновесия (время релаксации) очень мало по сравнению с периодом звуковой волны, то коэффициент О. в. h' не зависит от частоты. Если же при распространении звука термодинамическое равновесие нарушается, то h' принимает аномально большие значения и становится функцией частоты звука. В этом случае в среде возникают процессы восстановления равновесия, т. н. процессы релаксации , сопровождаемые необратимым переходом механической энергии деформации в теплоту.

Для определения коэффициента О. в. обычно пользуются данными по поглощению и дисперсии звука . Величина h' зависит от температуры и давления: она обычно уменьшается при повышении температуры и увеличивается при повышении давления. Величина О. в. в жидкостях обычно больше, чем О. в. в газах, в среднем на 1—3 порядка.

Лит.: Ландау Л. Д. и Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1954, § 78; Физическая акустика, под ред. У. Мэзона, т. 2, ч. А, Свойства газов, жидкостей и растворов, пер. с англ., М., 1968.

А. Л. Полякова.

Объёмная си'ла, сила, действующая на все частицы (элементарные объёмы) данного тела и пропорциональная массе частицы; то же, что массовая сила. Пример О. с. — силы тяготения. Предел отношения геометрической суммы О. с., действующих на частицу, к её объёму, при стягивании последнего в точку, называется напряжением О. с. в данной точке.

Объёмная штампо'вка, технологический процесс кузнечно-штамповочного производства , заключающийся в изменении простейших объёмных заготовок (цилиндрической, призматической и др. формы) в более сложные изделия, форма которых соответствует полости специализированных инструментов — штампов . О. ш. как процесс перераспределения металла заготовки происходит в результате пластической деформации (см. Обработка металлов давлением ).

Основные операции О. ш.— осадка, высадка, протяжка, выдавливание, гибка, плющение, калибровка, образование выступов, утолщений, углублений, осуществляемые на кузнечно-прессовых машинах — молотах , прессах и машинах специального назначения. Из штампованных поковок после обработки резанием и термической обработки получают различные детали: шатуны, коленчатые валы, рычаги, зубчатые колёса, лопатки турбин, крепёжные детали, шары, ролики и кольца подшипников и др.

Различают холодную и горячую О. ш. Холодная штамповка осуществляется без нагрева. Исходный материал — калиброванные прутки, нарезаемые на мерные (штучные) заготовки, или проволока в бунтах. Масса получаемых изделий от нескольких г до неск. кг ; точность по 3—2-му классам; шероховатость поверхности соответствует 7—10-му классам чистоты. Холодной О. ш. получают ответственные детали с высокими и стабильными механическими свойствами, что объясняется отсутствием рекристаллизации в металле и упрочнением. Т. к. заготовки не нагреваются, на поверхности поковок не происходит образования окалины, обезуглероживания, обесцинкования и т.п., что улучшает качество поковок в целом и сокращает припуски на дальнейшую обработку. В ряде случаев поковки не требуют дополнительной обработки, являясь готовыми деталями (коэффициент использования металла составляет 1). Однако для осуществления холодной О. ш. требуются значительные усилия — до 2500 Мн/м 2 (1 Мн = 100 тс ) и более, что отрицательно влияет на стойкость штампов. Существенно снизить усилия (в 10—15 раз) позволяет нагрев заготовок, т. е. горячая О. ш.