БСЭ БСЭ - Большая Советская Энциклопедия (ОБ)

С. М. Лейтес.

Обме'н телегра'фный, суммарное количество телеграмм, принятых за определённый промежуток времени (час, сутки, месяц и т.д.) по какой-либо линии телеграфной связи, каким-либо предприятием связи или всей телеграфной сетью. Наибольший суточный О. т. — в дневной период (от 12—14 часов до 18—20 часов), наименьший — в ночной (от 23 часов до 7—8 часов следующих суток); дни наименьшего обмена — суббота, воскресенье и понедельник (в воскресенье О. т. составляет примерно половину среднесуточного О. т. за неделю); месяцы повышенного О. т. — апрель, июль, август, ноябрь и декабрь.

Обме'нное взаимоде'йствие, специфическое взаимное влияние одинаковых, тождественных, частиц, эффективно проявляющееся как результат некоторого особого взаимодействия. О. в. — чисто квантовомеханический эффект, не имеющий аналога в классической физике (см. Квантовая механика ). Вследствие квантовомеханического принципа неразличимости одинаковых частиц ( тождественности принципа ) волновая функция системы должна обладать определенной симметрией относительно перестановки двух одинаковых частиц, т. е. их координат и спинов : для частиц с целым спином — бозонов — волновая функция системы не меняется при такой перестановке (является симметричной), а для частиц с полуцелым спином — фермионов — меняет знак (является антисимметричной). Если силы взаимодействия между частицами не зависят от их спинов, волновую функцию системы можно представить в виде произведения двух функций, одна из которых зависит только от координат частиц, а другая — только от их спинов. В этом случае из принципа тождественности следует, что координатная часть волновой функции, описывающая движение частиц в пространстве, должна обладать определённой симметрией относительно перестановки координат одинаковых частиц, зависящей от симметрии спиновой функции. Наличие такой симметрии означает, что имеет место определённая согласованность, корреляция, движения одинаковых частиц, которая сказывается на энергии системы (даже в отсутствие каких-либо силовых взаимодействий между частицами). Поскольку обычно влияние частиц друг на друга является результатом действия между ними каких-либо сил, о взаимном влиянии одинаковых частиц, вытекающем из принципа тождественности, говорят как о проявлении специфического взаимодействия — О. в. Возникновение О. в. можно проиллюстрировать на примере атома гелия (впервые это было сделано В. Гейзенбергом в 1926). Спиновые взаимодействия в лёгких атомах малы, поэтому волновая функция Y двух электронов в атоме гелия может быть представлена в виде:

Y = Ф ( r 1, r 2 )c( s 1, s 2 ), (1)

где Ф ( r 1, r 2 ) — функция от координат r 1, r 2 электронов, а c( s 1, s 2 ) — от проекции их спинов s 1, s 2 на некоторое направление. Т. к. электроны являются фермионами, полная волновая функция y должна быть антисимметричной. Если суммарный спин 5 обоих электронов равен нулю (спины антипараллельны — парагелий), то спиновая функция c антисимметрична относительно перестановки спиновых переменных и, следовательно, координатная функция Ф должна быть симметрична относительно перестановки координат электронов. Если же полный спин системы равен 1 (спины параллельны — ортогелий), то спиновая функция симметрична, а координатная — антисимметрична. Обозначая через y п ( r 1 ), y п' ( r 2 ) волновые функции отдельных электронов в атоме гелия (индексы n , n' означают набор квантовых чисел, определяющих состояние электрона в атоме), можно, пренебрегая сначала взаимодействием между электронами, записать координатную часть волновой функции в виде:

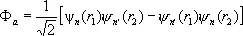
для случая S = 1, (2)

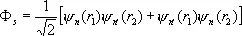
для случая S = 0 (2')

(множитель 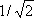введён для нормировки волновой функции). В состоянии с антисимметричной координатной функцией Ф а ср. расстояние между электронами оказывается бо'льшим, чем в состоянии с симметричной функцией Ф S ; это видно из того, что вероятность |Y| 2= |Ф а | 2|c S| 2нахождения электронов в одной и той же точке r 1 = r 2для состояния Ф а равна нулю. Поэтому средняя энергия кулоновского взаимодействия (отталкивания) двух электронов оказывается в состоянии Ф а меньшей, чем в состоянии Ф S . Поправка к энергии системы, связанная с взаимодействием электронов, определяется по теории возмущении и равна:

Е В3 = К ± А , (3)

где знаки ± относятся соответственно к симметричному Ф S и антисимметричному Ф а координатным состояниям,

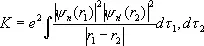(4)

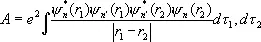
(dt = dxdydz — элемент объёма). Величина К имеет вполне наглядный классический смысл и соответствует электростатическому взаимодействию двух заряженных «облаков» с плотностями заряда е çy n(r 1)ç 2и е çy n ¢(r 2)ç 2. Величину А , называется обменным интегралом, можно интерпретировать как электростатическое взаимодействие заряженных «облаков» с плотностями заряда е y n*(r 1)y n¢(r 1) и е y n¢*(r 1)y n¢(r 2) y n(r 2), т. е. когда каждый из электронов находится одновременно в состояниях y nи y n¢ (что бессмысленно с точки зрения классической физики). Из (3) следует, что полная энергия пара- и ортогелия с электронами в аналогичных состояниях отличается на величину 2 А . Т. о., хотя непосредственно спиновое взаимодействие мало и не учитывается, тождественность двух электронов в атоме гелия приводит к тому, что энергия системы оказывается зависящей от полного спина системы, как если бы между частицами существовало дополнительное, обменное, взаимодействие. Очевидно, что О. в. в данном случае является частью кулоновского взаимодействия электронов и явным образом выступает при приближённом рассмотрении квантовомеханической системы, когда волновая функция всей системы выражается через волновые функции отдельных частиц (в частности, в приближении Хартри — Фока; см. Самосогласованное поле ).

О. в. эффективно проявляется, когда «перекрываются» волновые функции отдельных частиц системы, т. е. когда существуют области пространства, в которых с заметной вероятностью может находиться частица в различных состояниях движения. Это видно из выражения для обменного интеграла А : если степень перекрытия состояний y n*(r) и y n¢(r) незначительна, то величина А очень мала.