БСЭ БСЭ - Большая Советская Энциклопедия (ОБ)
- Название:Большая Советская Энциклопедия (ОБ)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ОБ) краткое содержание
Большая Советская Энциклопедия (ОБ) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Обобщённые координаты
Обобщённые координа'ты, независимые между собой параметры q i ( r = 1, 2,..., s) любой размерности, число которых равно числу s степеней свободы механич. системы и которые однозначно определяют положение системы. Закон движения системы в О. к. даётся s уравнениями вида q i= q i ( t ) , где t — время. О. к. пользуются при решении многих задач, особенно когда система подчинена связям, налагающим ограничения на её движение. При этом значительно уменьшается число уравнений, описывающих движение системы, по сравнению, например, с уравнениями в декартовых координатах (см. Лагранжа уравнения в механике). В системах с бесконечно большим числом степеней свободы (сплошные среды, физические поля) О. к. являются особые функции пространственных координат и времени, называются потенциалами, волновыми функциями и т.п.
Обобщённые силы
Обобщённые си'лы, величины, играющие роль обычных сил, когда при изучении равновесия или движения механической системы её положение определяется обобщёнными координатами . Число О. с. равно числу s степеней свободы системы; при этом каждой обобщённой координате q i соответствует своя О. с. Q i. Значение О. с. Q i, соответствующей координате q i , можно найти, вычислив элементарную работу dA 1всех сил на возможном перемещении системы, при котором изменяется только координата q i , получая приращение dq 1 . Тогда dA 1= Q 1dq 1 , т.е. коэффициент при dq i в выражении dA 1 и будет О. с. Q 1. Аналогично вычисляются Q 2, Q 3,..., Q s . Например, если для лебёдки ( рис. ) вместе с поднимаемым ею на тросе грузом весом Р (система с одной степенью свободы) принять за обобщённую координату q i угол j поворота вала лебёдки и если к валу приложены вращающий момент М вр и момент сил трения М тр , то в данном случае dA 1 = ( М вр—М тр—Pr )dj, где r — радиус вала (весом троса пренебрегаем). Следовательно, для этой системы О. с., соответствующей координате j, будет Q 1=М вр—М тр — Pr .
Размерность О. с. зависит от размерности обобщённой координаты. Если размерность q i— длина, то Q i имеет размерность обычной силы; если q i— угол, то Q i имеет размерность момента силы и т.д. При изучении движения механической системы О. с. входят вместо обычных сил в Лагранжа уравнения механики, а при равновесии все О. с. равны нулю. Например, для рассмотренной выше лебёдки при равномерном подъёме груза должно быть Q i = 0, т. е. М вр= М тр+ Pr .
С. М. Тарг.
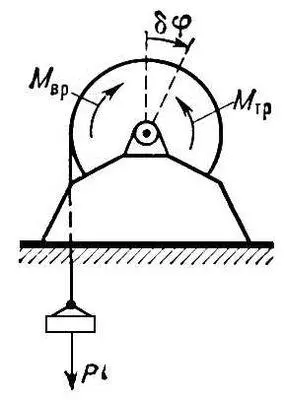
Рис. к ст. Обобщённые силы.
Обобщённые функции
Обобщённые фу'нкции, математическое понятие, обобщающее классическое понятие функции . Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие О. ф., с одной стороны, даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки (пространственная), плотность простого или двойного слоя, интенсивность мгновенного источника и т.д. С другой стороны, в понятии О. ф. находит отражение тот факт, что реально нельзя измерить значение физич. величины в точке, а можно измерять лишь её средние значения в достаточно малых окрестностях данной точки. Таким образом, О. ф. служат удобным аппаратом для описания распределений различных физических величин. Поэтому в иностранной литературе О. ф. называют распределениями.
О. ф. были введены впервые в конце 20-х гг. 20 в. П. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие дельта-функции и её производных. Основы математической теории О. ф. были заложены С. Л. Соболевым в 1936 при решении Коши задачи для гиперболич. уравнений, а в послевоенные годы французский математик Л. Шварц дал систематическое изложение теории О. ф. В дальнейшем теорию О. ф. интенсивно развивали многие математики, главным образом в связи с потребностями математической физики. Теория О. ф. имеет многочисленные применения и всё шире входит в обиход физика, математика и инженера.
Формально О. ф. определяются как линейные непрерывные функционалы над тем или иным линейным пространством основных функций j(x) . Основным пространством функций является, например, совокупность бесконечно дифференцируемых финитных функций, снабженная надлежащей сходимостью (или, точнее, топологией). При этом обычные локально суммируемые функции f (x) отождествляются с функционалами (регулярными О. ф.) вида
( f, j ) = ò f (x)j(x) dx . (1)
Произвольная О. ф. f определяется как функционал f’ , задаваемый равенством
(f¢, j) = ‑ (f, j¢). (2)
При таком соглашении каждая О. ф. бесконечно дифференцируема (в обобщённом смысле). Равенство (2) в силу (1) есть не что иное, как обобщение формулы интегрирования по частям для дифференцируемых в обычном смысле функций f (x) , так что в этом случае оба понятия производной совпадают.
Сходимость на (линейном) множестве О. ф. вводится как слабая сходимость функционалов. Оказывается, что операция дифференцирования О. ф. непрерывна, а сходящаяся последовательность О. ф. допускает почленное дифференцирование бесконечное число раз.
Вводятся и другие операции над О. ф., например свёртка функций , Фурье преобразование , Лапласа преобразование . Теория этих операций приобретает наиболее простую и законченную форму в рамках понятия О. ф., расширяющих возможности классического математического анализа. Поэтому использование О. ф. существенно расширяет круг рассматриваемых задач и к тому же приводит к значительным упрощениям, автоматизируя элементарные операции.
Примеры. 1) d-функция Дирака:
(d, j) = j(0),
описывает плотность массы (заряда) 1, сосредоточенной в точке х = 0, единичный импульс.
2) q (x) — функция Хевисайда: q(x) = 0, х £ 0, q(x) = 1, x > 0, q' = d;
производная от неё равна единичному импульсу.
3) —d' — плотность диполя момента 1 в точке х = 0, ориентированного вдоль оси х .
4) md s— плотность простого слоя на поверхности S с поверхностной плотностью m:
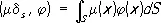
5) 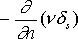 — плотность двойного слоя на поверхности S с поверхностной плотностью момента n диполей, ориентированных вдоль направления нормали n :
— плотность двойного слоя на поверхности S с поверхностной плотностью момента n диполей, ориентированных вдоль направления нормали n :
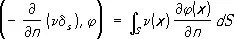 .
.
Интервал:
Закладка:
