БСЭ БСЭ - Большая Советская Энциклопедия (ОБ)

Функциональная специализация клеток в большой степени сопряжена с изменениями химического состава О. Так, одревеснение обусловлено появлением в ней лигнина (в особенности в древесине и склеренхиме ), что повышает твёрдость оболочки; рост клетки прекращается. Опробкование связано с отложением в ней суберина, не проницаемого для жидкостей и газа, что приводит к гибели протопласта ( пробка , экзодерма ). Кутин обусловливает кутинизацию О., образуя на наружной поверхности клеток эпидермиса плёнку — кутикулу , защищающую ткани от перегревания и испарения. Накопление солей кальция (красные водоросли, кувшинки) или кремнезёма (диатомовые водоросли, эпидермис хвощей, злаков) вызывает минерализацию О. Превращение пектиновых веществ и целлюлозы в слизи , удерживающие влагу, приводит к ослизнению (ослизнение семенной кожуры облегчает прорастание семени). При повреждении на поверхности стволов вишни, миндаля, акации и др. растений выделяются сходные со слизями в химическом отношении камеди , используемые для приготовления клея и применяемые в медицине.

Лит.: Раздорский В. Ф., Анатомия растений, М., 1949; Фрей-Висслинг А., Мюлеталер К., Ультраструктура растительной клетки, пер. с англ., М., 1968; Биохимия растений, пер. с англ., М., 1968; Эсау К., Анатомия растений, пер. с англ., М., 1969.

Л. И. Лотова.

О. животной клетки — специализированный слой на её поверхности. В составе О. различают плазматическую мембрану, или плазмалемму,— субмикроскопическую структуру толщиной ок. 100 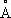, и собственно О. Плазматическая мембрана имеется у всех клеток, она играет важную роль в обмене веществ между клеткой и внешней средой (обладает избирательной проницаемостью), движении клеток и сцеплении их друг с другом; состоит из белков и липидов; в зависимости от природы клеток и их физиологического состояния образует выросты (см. Микроворсинки ) и впячивания (см. Пиноцитоз ). Собственно О. имеется не у всех животных клеток; она отличается большим разнообразием, может выполнять функцию наружного скелета клетки (пелликула простейших, хитиновая кутикула членистоногих), играет защитную роль (многослойная О. яйцеклеток, О. цист); состоит главным образом из углеводов и их соединений с белками, а также липидов и неорганических веществ, секретируется как самой клеткой, так и окружающими клетками этой и др. тканей.

Лит. см. при ст. Клетка.

Т. Б. Айзенштадт.

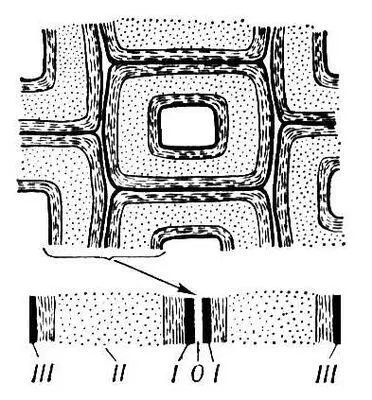
Оболочка растительной клетки с трёхслойной вторичной оболочкой: О — срединная пластинка; I — первичная оболочка; II — вторичная оболочка, состоящая из трёх слоев; III — третичная оболочка.

Оболо'чкав технике и теории упругости, твёрдое тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с двумя другими размерами. Поверхность, делящая пополам толщину О., называется срединной поверхностью; в зависимости от её очертания различают цилиндрическую О. с сечением круговой, эллиптической и др. формы; конические, тороидальные и т.д. ( рис. 1 ). О. классифицируются также по полной кривизне поверхности — т. н. гауссовой кривизне: положительной — сферические, эллипсоидальные и др. О., нулевой — цилиндрические, конические; отрицательной — гиперболические параболоиды. О. могут быть постоянной и переменной толщины. Они подразделяются на одно-, двух- и многослойные. В зависимости от материала О. бывают изотропными либо анизотропными. Выполняются О. из железобетона, стали, дерева, лёгких сплавов, пластмасс и др. строительных материалов.

Под воздействием внешних нагрузок в О. возникают внутренние усилия, равномерно распределённые по толщине (т. н. мембранные напряжения, или напряжения в срединной поверхности), и усилия изгиба, образующие в сечениях О. изгибающие и крутящие моменты, а также поперечные силы. Благодаря наличию мембранных усилий О. сочетают значительную жёсткость и прочность со сравнительно малым весом, что отличает их от пластинок. Если напряжениями изгиба при расчёте можно пренебречь, то О. называется безмоментной. Наличие моментов характерно для участков О., примыкающих к краям (так называемый краевой эффект).

Если напряжения лежат в пределах пропорциональности для материала О., то методы расчёта О. основываются на зависимостях упругости теории . Чаще всего для тонких О. применяют гипотезу Кирхгофа — Лява, по которой любое прямое волокно, нормальное к срединной поверхности до деформации, остаётся прямым и нормальным к срединной поверхности и после деформации; вместе с тем его длина остаётся неизменной. Кроме того, считают, что нормальными напряжениями в направлении, перпендикулярном к срединной поверхности, можно пренебречь по сравнению с основными напряжениями. При этом общая трёхмерная задача теории упругости переходит в двумерную. Решение задачи сводится к интегрированию системы дифференциальных уравнений в частных производных высокого порядка при краевых условиях, определяемых характером сопряжения О. с другими частями конструкции. В статическом расчёте О. на прочность и жёсткость должны быть определены напряжения, деформации и перемещения различных точек О. в зависимости от заданной нагрузки. Как правило, в расчётах на прочность прогибы О. (перемещения вдоль нормали к срединной поверхности) могут считаться малыми по сравнению с толщиной О.; тогда соотношения между перемещениями и деформациями являются линейными; соответственно линейными (для упругой задачи) будут основные дифференциальные уравнения.

О. часто приходится подкреплять ребрами (в основном для обеспечения устойчивости их деформации), например фюзеляжи и крылья самолётов, некоторые типы тонкостенных перекрытий и др.

Важным для О. является расчёт на устойчивость (см. Устойчивость упругих систем ). Специфическая особенность тонкостенных О. — потеря устойчивости хлопком, или прощёлкиванием, выражающаяся в резком переходе от одного устойчивого равновесного состояния к другому; этот переход наступает при различных нагрузках, в зависимости от исходных несовершенств формы оболочки, начальных напряжений и т.д. В случае прощёлкивания прогибы оказываются соизмеримыми с толщиной О.; анализ поведения О. должен основываться при этом на уравнениях, являющихся уже нелинейными.

В задачах динамики О. рассматриваются периодические колебания и нестационарные процессы, связанные с быстрым или ударным нагружением. При обтекании О. потоком жидкости либо газа могут наступить неустойчивые (автоколебательные) режимы, определение которых является предметом гидро- или аэроупругости. Особый раздел теории колебаний, имеющий важные приложения, представляет исследование нелинейных колебаний О. При рассмотрении динамических процессов в О. соотношения, основанные на гипотезе Кирхгофа — Лява, не всегда оказываются приемлемыми; тогда переходят к дифференциальным уравнениям более сложной структуры.