БСЭ БСЭ - Большая Советская Энциклопедия (ОД)

Однопо'лые цветки', цветки, в которых имеются только тычинки, но нет пестика (пестиков) или имеется только пестик (пестики), но нет тычинок. В первом случае цветки называют тычиночными (мужскими), во втором — пестичными (женскими). Во многих О. ц. не функционирующие органы др. пола сохраняются в редуцированном состоянии, что указывает на их происхождение от обоеполых цветков . Такие цветки называют функционально-мужскими или функционально-женскими. Распределение О. ц. на растениях варьирует (см. Однодомные растения , Двудомные растения , Многодомные растения ).

Однопо'люсное телеграфи'рование, метод телеграфирования постоянным электрическим током, при котором передаваемые по линии связи кодовые комбинации состоят из посылок тока (например, положительной полярности) и бестоковых интервалов. При О. т. в качестве передатчика используется передатчик стартстопного телеграфного аппарата , а в качестве приёмника — его неполяризованный электромагнит. В отличие от двухполюсного телеграфирования , при О. т. по однопроводной воздушной линии связи электромагнит более чувствителен к утечке тока в линии, особенно при сырой погоде, и к наводимым в ней (индуктивным) помехам. Поэтому на воздушных линиях связи О. т. применяют только тогда, когда их протяжённость невелика (200—350 км ). О. т. используют также на линиях, соединяющих телеграфы с городскими отделениями связи.

Однопрохо'дные, отряд млекопитающих; то же, что клоачные .

Одноро'дная фу'нкция, функция одного или нескольких переменных, удовлетворяющая следующему условию: при одновременном умножении всех аргументов функции на один и тот же (произвольный) множитель значение функции умножается на некоторую степень этого множителя, т. е. для О. ф. f (x, y,..., u) при всех значениях х, у,..., u и любом l должно иметь место равенство:

f (l x , l у ,..., l u ) = l n f ( х, y,..., u ),

где n — некоторый определённый показатель («показатель однородности», или «измерение О. ф.»). Например, функции

х 2— 2у 2; ( x— y —3 z )/ z 2 + xyz 2 ;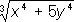

суть однородные с измерениями, соответственно, 2, —1, 4/ 3. Из дифференциальных свойств О. ф. отметим одно (теорема Эйлера), вполне характеризующее О. ф. измерения n, а именно: если в выражении полного дифференциала 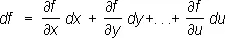такой функции f ( x, у,..., u ) заменить дифференциал каждого независимого переменного самим этим переменным, то получают функцию f ( x, у,..., u ), умноженную на показатель однородности:

.

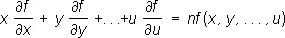О. ф. часто встречаются в геометрических формулах. В соотношении х =f ( а, b, ..., l ), где а, b,..., l — длины отрезков, измеренные одним и тем же произвольным масштабом, правая часть должна быть О. ф. (измерения 1, 2 или 3, смотря по тому, означает ли х длину, площадь или объём). Например, в формуле для объёма

усечённого конуса правая часть — О.ф. h , R и r измерения 3.

Одноро'дное уравне'ние, уравнение, не меняющее своего вида при одновременном умножении всех (или только некоторых) неизвестных на одно и то же произвольное число. Во втором случае уравнение называется однородным по отношению к соответствующим неизвестным. Так, ху + yz + zx = 0 есть О. у. по отношению ко всем неизвестным, уравнение 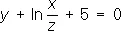однородно по отношению к х и z. Левая часть о. у. является однородной функцией . Уравнение

a 0(x) y (n)+ a 1(x) y (n-1)+ ... + a n(x) y = 0,

называемое линейным однородным дифференциальным уравнением, однородно по отношению к у, у', ..., y (n-1), y (n). Уравнение у' = f (х, у), где f (x, y) = f ( l x, l у) при любом l [ f (x, y) — однородная функция со степенью однородности 0], называется дифференциальным уравнением, однородным по отношению к переменным x и у . Пример: .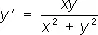

Одноро'дные координа'тыточки, прямой и т.д., координаты, обладающие тем свойством, что определяемый ими объект не меняется, когда все координаты умножаются на одно и то же число. Например, О. к. точки М на плоскости могут служить три числа: X , Y, Z, связанные соотношением X : Y : Z = х : у : 1, где х и у — декартовы координаты точки М . Введение О. к. позволяет добавить к точкам евклидовой плоскости точки с третьей О. к., равной нулю (т. н. бесконечно удалённые точки), что важно для проективной геометрии . См. также Координаты .

Односвя'зная о'бласть, плоская область , обладающая тем свойством, что для любой замкнутой непрерывной кривой, принадлежащей области, часть плоскости, ограниченная этой кривой, принадлежит области. Например, внутренность круга, квадрата, треугольника — О. о. Внутренность кругового кольца не является О. о. — это двусвязная область (см. Многосвязная область ).

Односемядо'льные, односемянодольные, класс покрытосеменных растений; то же, что однодольные .

Односторо'ннее движе'ние, метод регулирования дорожного движения путём использования всей ширины проезжей части улицы или дороги для движения транспортных средств только в одном направлении. Иногда при организации О. д. сохраняют встречное движение маршрутных автобусов или троллейбусов; в некоторых случаях режим О. д. вводят на определённые промежутки времени. При введении О. д. пропускная способность проезжей части и скорость движения возрастают в среднем на 10—12%, а количество дорожно-транспортных происшествий существенно уменьшается.

Улицы с О. д. существовали ещё в древней Помпее. В 1906 О. д. было введено на улицах г. Филадельфия (США). О. д. широко распространено во многих городах мира; в частности, в Париже примерно на 30% улиц организовано О. д. В ряде городов СССР (Москва, Ленинград, Рига, Вильнюс, Баку, Куйбышев, Горький и др.) на улицах также принято О. д.