БСЭ БСЭ - Большая Советская Энциклопедия (ОП)

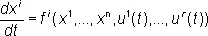(3)

x i ( t 0) = x i 0,

i = 1,..., n ,

удовлетворяет условию x i ( t 1) = x i 1. Качество этого управления будем оценивать значением функционала

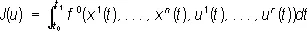, (4)

где 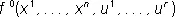— заданная функция. Задача О. у. состоит в отыскании такого реализующего цель управления, для которого функционал (4) принимает наименьшее возможное значение. Т. о., математическая теория О. у. — это раздел математики, рассматривающий неклассические вариационные задачи отыскания экстремумов функционалов на решениях уравнений, описывающих управляемые объекты, и управлений, на которых реализуется экстремум.

Сформулируем для поставленной задачи необходимое условие оптимальности управления.

Принцип максимума Понтрягина. Пусть вектор-функция

u = u ( t ) = ( u 1( t ),..., u r ( t )), t £ t 0 £ t 1, (5)

– оптимальное управление, а вектор-функция

x = x ( t ) = ( x 1( t ),..., x n ( t )), t £ t 0 £ t 1,

– соответствующее ему решение задачи (3). Рассмотрим вспомогательную линейную систему обыкновенных дифференциальных уравнений

, (6)

k = 0, 1,..., n ,

и составим функцию

Н (y, х , u ) = ,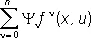

зависящую, помимо х и u , от вектора y = (y 0, y 1,..., y n ). Тогда у линейной системы (6) существует такое нетривиальное решение

y = y( t ) = (y 0( t ), y 1( t ),..., y n ( t )),

t £ t 0 £ t 1,

что для всех точек t из отрезка [ t 0, t 1], в которых функция (5) непрерывна, выполнено соотношение

мах Н (y( t ), х ( t ), u ) = Н (y( t ), x ( t ), u ( t )) = 0,

u Î U

причём y 0(t) º const £ 0.

К виду (1) обычно приводятся уравнения движения в случае управляемых механических объектов с конечным числом степеней свободы. В многочисленных реальных ситуациях возникают и иные постановки задач О. у., отличающиеся от приведённой выше: задачи с фиксированным временем, когда продолжительность процесса заранее задана, задачи со скользящими концами, когда про начальное и конечное состояния известно, что они принадлежат некоторым множествам, задачи с фазовыми ограничениями, когда решение задачи (3) в каждый момент времени должно принадлежать фиксированному замкнутому множеству, и др. В задачах механики сплошных сред характеризующая состояние управляемого объекта величина х является функцией уже не только времени, но и пространственных координат (например, величина х может описывать распределение температуры в теле в данный момент времени), а закон движения будет дифференциальным уравнением с частными производными. Часто приходится рассматривать управляемые объекты, когда независимая переменная принимает дискретные значения, а закон движения представляет собой систему конечно-разностных уравнений. Наконец, отдельную теорию составляет О. у. стохастическими объектами.

Лит.: Математическая теория оптимальных процессов, 2 изд.. М., 1969 (авт. Л. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко); Красовский Н. Н., Теория управления движением, М., 1968; Моисеев Н. Н., Численные методы в теории оптимальных систем, М., 1971.

Н. Х. Розов.

Оптима'льные це'ныпри социализме, цены, получаемые в процессе расчёта оптимальною плана производства и потребления продукции на одном и том же массиве экономической информации методами математического программирования (см. Планирование оптимальное ). Применение О. ц. в масштабах народного хозяйства возможно только в условиях социалистической системы хозяйства. Действие основного экономического закона социализма позволяет представить народнохозяйственное планирование в экстремальной динамической задаче математического программирования.

О. ц. обладают следующими свойствами: обеспечивают хозрасчётное стимулирование выполнения плановых заданий в натуральном выражении (все производственные способы, вошедшие в оптимальный план и измеренные в О. ц., рентабельны; все отвергнутые хозяйственные решения убыточны); оценивают затраты отдельных хозяйственных звеньев с позиций их народно-хозяйственной эффективности (О. ц. включают не только прямые затраты на производство конкретного продукта, но и всю совокупность дополнительных затрат, которые общество вынуждено нести в др. сферах в связи с производством данного продукта); характеризуют уменьшение или увеличение общественных затрат и результатов только в пределах небольших изменений производства и потребления продукции. Последнее свойство О. ц. позволяет использовать их для оценки микроэкономических процессов.

Н. Я. Петраков.

Оптима'льный(от лат. optimus — наилучший), наиболее благоприятный, лучший из возможных (например, О. решение).

Оптима'ты(лат. optimates — знатные, от optimus — наилучший), идейно-политическое течение в Римской республике (конца 2—1 вв. до н. э.), отражавшее интересы нобилитета и противостоявшее популярам .

Оптиме'тр(от греч. optós — видимый и... метр ), прибор для измерения линейных размеров (относительным методом), преобразовательным элементом в котором служит рычажно-оптический механизм. Рычажной передачей является в механизме качающееся зеркало, оптическим преобразователем — автоколлимационная трубка (см. Автоколлиматор ). Качающееся зеркало в измерительных приборах впервые применил немецкий инженер И. Сакстон в 1837. Прибор, в котором использовалось качающееся зеркало с автоколлимационной зрительной трубкой, впервые изготовлен в 1925 (фирма Цейс, Германия). Выпускаются вертикальные и горизонтальные О., различающиеся только конструкцией станины. Оптический преобразователь О. — трубка может иметь окулярный или проекционный отсчёт ( рис. ). В трубке с проекционным отсчётом освещается лампой пластина, на которой с одной стороны от центра нанесена шкала, а с другой — индекс. В окулярной трубке пластина освещается «зайчиком» от специального зеркала. Изображение шкалы попадает сначала на неподвижное зеркало, а затем на зеркало, которое качается и занимает различные угловые положения в зависимости от положения измерительного стержня. В трубке с окулярным отсчётом нет неподвижного зеркала. После отражения от зеркала изображение шкалы попадает на вторую половину пластины (накладывается на индекс). Вторичное изображение шкалы, которое смещается относительно неподвижного индекса при перемещении стержня, проектируется с помощью зеркал на экран в проекционной трубке О. (или рассматривается через окуляр). Трубка О. имеет шкалу с ценой деления 1 мкм , предел измерения по шкале ± 100 мкм .