БСЭ БСЭ - Большая Советская Энциклопедия (ОС)

Основа'ния, химические соединения, содержащие гидроксильную группу OH и способные диссоциировать в водном растворе с образованием гидроксильных ионов OH —. По степени диссоциации различают слабые О., например NH 4OH, и сильные О., например NaOH, Ca (OH) 2. Хорошо растворимые в воде О. называются щелочами. См. также Кислоты и основания .

Основа'ния матема'тики, совокупность понятий, концепций и методов, с помощью которых строятся различные математические дисциплины, а также комплекс математических и философских теорий и направлений, посвященных исследованию этих понятий, концепций и методов. См. ст. Математика , раздел Современная математика.

Основа'ния сооруже'ний, массивы горных пород, непосредственно воспринимающие нагрузки от сооружений. В О. с. возникают деформации от нагружения их сооружениями. О. с. могут служить все виды горных пород: скальные (скальные О. с.) и рыхлые (грунтовые О. с., см. Грунт ). О. с., образуемые горными породами в их природном, естественном залегании, называется естественными основаниями; если же для устройства оснований горные породы уплотняются или закрепляются, то такие О. с. называются искусственно укреплёнными основаниями. О. с. воспринимают нагрузку, передаваемую на них сооружениями через фундаментную конструкцию (см. Фундаменты зданий и сооружений ). Правильный выбор вида основания и фундамента, помимо обеспечения долговечности сооружения и нормальных условий его эксплуатации, имеет большое экономическое значение. В современном строительстве затраты на устройство оснований и фундаментов составляют 15—20% стоимости всего сооружения, трудовые затраты 12—15% общих затрат труда. Возведение подземной части сооружения занимает 20—35% времени, отводимого на строительство объекта в целом. В СССР совершенствование проектирования (и устройства) О. с. достигнуто в результате замены расчёта О. с. по допускаемым давлениям (не учитывавшего в полной мере условий взаимодействия сооружения и его основания) расчётом по предельным состояниям (см. Предельное состояние ), а также за счёт типизации конструктивных элементов фундаментов и применения эффективных методов работ. Метод расчёта О. с. по предельным состояниям, являющийся достижением сов. школы механики грунтов и фундаментостроения, исходит из объективных характеристик грунтов, условий их залегания и особенностей проектируемого сооружения. Использование этого метода обеспечивает повышение эксплуатационных качеств сооружений, полное использование несущей способности грунтов основания и более рациональное расходование материалов. При строительстве на грунтовых основаниях рассматривают 2 вида предельных состояний: по несущей способности основания (ограничение нагрузки пределами, гарантирующими основание от разрушения) и по деформации основания (ограничение деформации надфундаментных конструкций при деформациях основания пределами, гарантирующими сохранение прочности и нормальных условий эксплуатации конструкций). Исчерпание несущей способности (потеря устойчивости) основания сопровождается образованием в грунте поверхностей скольжения, для которых соотношение между нормальными (s) и касательными (t) напряжениями от нагрузки сооружением и от собственного веса грунта выражается формулой Кулона: t = s tg j + с, где j и с — параметры грунта (угол внутреннего трения и сцепление), характеризующие его сопротивление сдвигу при данных условиях нагружения грунта. Опытами подтверждена правомерность использования формулы Кулона для большинства грунтов при давлении s до » 700 кн/м 2(7 кгс/см 2). Для сильно сжимаемых грунтов (с модулем деформации Е 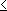5 Мн/м 2, или 50 кгс/см 2) зависимость t = f (s) криволинейна; в этих случаях для решения задач об устойчивости оснований применяются методы нелинейной механики грунтов.

Совместные деформации основания и сооружения и их предельные значения могут быть следующих видов: абсолютная осадка фундамента; средняя осадка сооружения; относительная неравномерность осадок соседних фундаментов; крен фундамента или сооружения в целом; относительный прогиб участка сооружения; относительный угол закручивания сооружения; горизонтальные перемещения фундамента или сооружения. Неравномерные деформации основания (изгиб, закручивание и т.п.) могут привести к повреждениям конструкций сооружения, в то время как равномерная осадка и крен сооружения оказывают влияние лишь на его эксплуатационного качества. Строительные нормы и правила устанавливают предельные значения отдельных видов деформаций оснований различных сооружений.

Осадки О. с. под отдельными фундаментами определяются соответствующими расчётными методами как осадки центров тяжести их подошвы. При балочных фундаментах или фундаментах в виде сплошных плит решают задачу расчёта конструкций на упругом (сжимаемом) основании, полагая S ( x, у ) = W ( x, у ), где S ( x, у ) — осадка поверхности грунта под фундаментом в точке с координатами х и у , контактирующей с подошвой фундамента, a W ( x, у ) — вертикальное перемещение точки подошвы фундамента с теми же координатами. Решение задачи основано на рассмотрении системы двух уравнений, описывающих изгиб конструкции сооружения и осадку основания при нагружении его фундаментом. Совместное решение уравнений изгиба фундаментной балки или плиты и осадки основания выполняется приближёнными методами. При этом широко используются ЭВМ. Применяя метод итерации (последовательного приближения), можно также получать решения при сложных закономерностях изменения свойств грунтов О. с. (как по глубине, так и по протяжённости), в том числе и нелинейных. Особые задачи расчёта и проектирования О. с. возникают в случаях, когда основание сложено: вечномёрзлыми грунтами (см. Многолетнемёрзлые горные породы ); грунтами повышенной деформативности (т. н. слабыми грунтами — илами, иловатыми и заторфованными); грунтами просадочными и набухающими при замачивании. Передача на О. с. нагрузки от сооружений со свайными фундаментами (см. Сваи , Свайный фундамент ) имеет также особый характер, учитываемый при расчёте устойчивости фундаментов. Однако нормативы предельных деформаций О. с. и при этой конструкции фундамента сохраняются те же. Скальные породы используются в качестве основания преимущественно при строительстве транспортных (например, опоры мостов) и гидротехнических (основания плотин) сооружений. При этом учитывают природную неоднородность скального основания (сложную ориентированность слоистой породы и различие механических свойств слоев), трещиноватость скальных грунтов и наличие в них в отдельных случаях пустот (см. Карст ). При строительстве гидротехнических сооружений возникает необходимость борьбы с фильтрацией воды в О. с., что требует уплотнения и закрепления грунтовых оснований или цементации трещиноватых скальных пород (см. Уплотнение грунтов ).