БСЭ БСЭ - Большая Советская Энциклопедия (ОС)

Соч.: Письма об эстетическом воспитании, 3 изд., М., 1908; Этюды о русских писателях, в. 1—5, СПБ, 1903—11; Из мира великих преданий, 12 изд., СПБ, 1911; Русские писатели, как воспитательно-образовательный материал для занятий с детьми и для чтения народу, 7 изд., СПБ, 1913; Беседы о преподавании словесности, 4 изд., СПБ, 1913; Выразительное чтение, 8 изд., М., 1916.

Лит.: Гречишникова А. Д., В. И. Водовозов и В. П. Острогорский, М., 1941; Роткович Я. А., Вопросы преподавания литературы. Историко-методические очерки, М., 1959.

Н. И. Якушин.

Острого'рскийГеоргий Александрович [р. 6(19).1.1902, Петербург], югославский византинист, действительный член Сербской АН (1948). Профессор Белградского университета (с 1933). С 1948 директор института византиноведения Сербской АН. Почётный член многих академий Европы. Автор работ по социально-экономической истории Византии и по истории византийско-сербских отношений. Общий курс О. по истории Византии (переведённый на многие европейские языки) пользуется значительным авторитетом. В отличие от большинства русских дореволюционных и современных византинистов Западной Европы и США, О. признаёт наличие в Византии феодализма как социально-экономической системы. Коренное изменение социально-политических отношений (утверждение свободного крестьянства, организация фем ) О. датирует 7 в. (в то время как многие историки — 8 — 1-й половиной 9 вв.). О. — сторонник теории непрерывности (от времён Римской империи) развития византийских городов.

Соч.: Сабрана дела, књ. 1—3, Београд, [1969—70]; Geschichte des byzantinischen Staates, Münch., 1963; Pour l’histoire de la féodalité byzantine, Brux., 1954.

Острого'ты,германское племя; см. Остготы .

Острогра'дскийМихаил Васильевич [12(24).9.1801, деревня Пашенная, ныне Полтавской области, — 20.12.1861(1.1.1862), Полтава], русский математик, академик Петербургской АН (1830). Учился в Харьковском университете (1816—20), а затем слушал в Париже (1822—28) лекции О. Коши , П. Лапласа , Ж. Фурье . Профессор офицерских классов Морского кадетского корпуса (с 1828), института корпуса инженеров путей сообщения (с 1830), Главного педагогического института (с 1832), Главного инженерного училища (с 1840), Главного артиллерийское училища (с 1841) в Петербурге. Основные работы относятся к математическому анализу, теоретической механике, математической физике; известен также работами по теории чисел, алгебре, теории вероятностей. О. решил (1826) важную задачу о распространении волн на поверхности жидкости, заключённой в бассейне, имеющем форму круглого цилиндра. В работах по теории распространения тепла в твёрдых телах и в жидкостях О. получил дифференциального уравнения распространения тепла и одновременно пришёл к ряду важнейших результатов в области математического анализа: нашёл формулу преобразования интеграла по объёму в интеграл по поверхности (см. Остроградского формула ), ввёл понятие сопряжённого дифференциального оператора, доказал ортогональность собственных функций данного оператора и сопряжённого, установил принцип разложимости функций в ряд по собственным функциям и принцип локализации для тригонометрических рядов. Теория распространения тепла в жидкости фактически впервые была построена О.; занимался также вопросами теории упругости, небесной механики, теории магнетизма и др.

Установленная О. (1828) формула преобразования интеграла по объёму в интеграл по поверхности была обобщена им (1834) на случай n -кратного интеграла. При помощи этой формулы О. нашёл вариацию кратного интеграла. О. дал (1836, опубликовано в 1838) вывод правила преобразования переменных интегрирования в двойных и тройных интегралах, метод интегрирования рациональных функций — выделение рациональной части интеграла (т. н. Остроградского метод ). Важные результаты были получены О. в теории дифференциальных уравнений, приближённом анализе.

В теоретической механике О. принадлежат фундаментальные результаты, связанные с развитием принципа возможных перемещений, вариационных принципов механики, а также с решением ряда частных задач; О. построена (1854) общая теория удара. В 40-х гг. 19 в. общий вариационный принцип почти одновременно был высказан для консервативных систем У. Гамильтоном и для неконсервативных систем О. В «Мемуаре о дифференциальных уравнениях, относящихся к проблеме изопериметров» (1850) О. обобщил эти результаты на общую изометрическую задачу вариационного исчисления. Большой интерес для своего времени имели работы О. по теории движения сферических снарядов в воздухе и выяснению влияния выстрела на лафет орудия.

О. был передовым учёным, стоял на позициях естественнонаучного материализма. Критерием ценности математических исследований для О. служила практика, возможность использовать полученные результаты в практической деятельности. Характерны в этом отношении его исследования по теории вероятностей. Одно из них, положившее начало статистическому методу браковки, проведено им с целью облегчения работы по проверке товаров, поставляемых армии. О. принадлежит также ряд популярных статей, педагогических исследований и превосходных для своего времени учебников. О. был членом многих иностранных академий.

Соч.: Полн. собр. трудов, т. 1—3, К., 1959—61.

Лит.: Гнеденко Б. В., Погребысскии И. Б., Михаил Васильевич Остроградский, М., 1963.

М. В. Остроградский.

Острогра'дского ме'тод,метод выделения рациональной части неопределённого интеграла

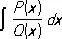
где Q ( x ) — многочлен степени п , имеющий кратные корни, а Р ( х ) — многочлен степени m £ n — 1.

О. м. позволяет алгебраическим путём представить такой интеграл в виде суммы двух слагаемых, из которых первое является рациональной функцией переменного х , а второе рациональной части не содержит. Имеет место равенство

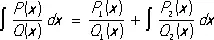(1)

где Q 1 , Q 2, P 1, P 2 — многочлены степеней соответственно n 1, n 2, m 1, m 2, причём n 1+ n 2 = n , m 1£ n 1— 1, m 2£ n 2— 1 и многочлен Q 2( x ) не имеет кратных корней. Многочлен Q 1( x ) является наибольшим общим делителем многочленов Q ( x ) и 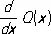, и, следовательно, явное выражение Q 1( x ) можно найти, например, с помощью Евклида алгоритма . Дифференцируя правую и левую части (1), получим тождество