БСЭ БСЭ - Большая Советская Энциклопедия (ПЛ)

При рассмотрении движения П. методами магнитной гидродинамики необходимо учитывать, что вмороженность поля может быть неполной; её степень определяется магнитным Рейнольдса числом .

Наиболее детальным методом описания П. является кинетический, основанный на использовании функции распределения частиц по координатам и импульсам f = f ( t, r, p ) . Импульс частицы p равен mu. В состоянии равновесия термодинамического эта функция имеет вид универсального Максвелла распределения , а в общем случае её находят из кинетического уравнения Больцмана :

.

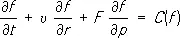Здесь F = e E+ ( e/c )[ u B ] — внешняя сила, действующая на заряженную частицу П., а член С ( f ) учитывает взаимные столкновения частиц. При рассмотрении быстрых движений П. столкновениями часто можно пренебречь, полагая С ( f ) » 0. Тогда кинетическое уравнение называется бесстолкновительным уравнением Власова с самосогласованными полями Е и В (они сами определяются движением заряженных частиц). Если П. полностью ионизована, т. е. в ней присутствуют только заряженные частицы, то их столкновения, ввиду преобладающей роли далёких пролётов (см. выше), эквивалентны процессу диффузии в пространстве импульсов (скоростей). Выражение С ( f ) для такой П. было получено Л. Д. Ландау и может быть записано в виде:

,

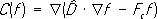где Ñ = 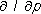— градиент в импульсном пространстве, 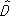— тензорный коэффициент диффузии в этом же пространстве, a F c— сила взаимного (так называемого «динамического») трения частиц.

При высоких температурах и низкой плотности можно пренебречь столкновениями частиц с частицами в П. Однако в случае, когда в П. возбуждены волны какого-либо типа (см. ниже), необходимо учитывать «столкновения» частиц с волнами. При не слишком больших амплитудах колебаний в П. подобные «столкновения», как и при далёких пролётах, сопровождаются малыми изменениями импульса частиц, и член С ( f ) с охраняет свой «диффузионный» вид с тем отличием, что коэффициент 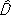определяется интенсивностью волн. Важнейшим результатом кинетического описания П. является учёт взаимодействия волны с группой так называемых резонансных частиц, скорости которых совпадают со скоростью распространения волны. Именно эти частицы могут наиболее эффективно обмениваться с волной энергией и импульсом. В 1946 Л. Д. Ландау предсказал возможность основанного на таком обмене «бесстолкновительного затухания» ленгмюровских волн, впоследствии обнаруженного в опытах с П. Если направить в П. дополнительный пучок частиц, то подобный обмен может приводить не к затуханию, а к усилению волн. Этот эффект в известном смысле аналогичен Черенкова — Вавилова излучению .

Колебания и неустойчивости плазмы.Волны в П. отличают их объёмный характер и разнообразие свойств. С помощью разложения в Фурье ряд любое малое возмущение в П. можно представить как набор волн простейшего синусоидального вида ( рис. 8 ). Каждая такая (монохроматическая) волна характеризуется определённой частотой w , длиной волны l и так называемой фазовой скоростью распространения u фаз. Кроме того, волны могут различаться поляризацией, т. е. направлением вектора электрического поля в волне. Если это поле направлено вдоль скорости распространения, волна называется продольной, а если поперёк — поперечной. В П. без магнитного поля возможны волны трёх типов: продольные ленгмюровские с частотой w o , продольные звуковые (точнее ионно-звуковые) и поперечные электромагнитные (световые или радиоволны). Поперечные волны могут обладать двумя поляризациями и могут распространяться в П. без магнитного поля, только если их частота w превышает плазменную частоту w o. В противоположном же случае w < w o преломления показатель П. становится мнимым, и поперечные волны не могут распространяться внутри П., а отражаются её поверхностью подобно тому, как лучи света отражаются зеркалом. Именно поэтому радиоволны с l > ~ 20 м отражаются ионосферой, что обеспечивает возможность дальней радиосвязи на Земле.

Однако при наличии магнитного поля поперечные волны, резонируя с ионами и электронами на их циклотронных частотах, могут распространяться внутри П. и при w < w o. Это означает появление ещё двух типов волн в П., называются альфвеновскими и быстрыми магнитозвуковыми. Альфвеновская волна представляет собой поперечное возмущение, распространяющееся вдоль магнитного поля со скоростью u a = В/ ( M i— масса ионов). Её природа обусловлена «вмороженностью» и упругостью силовых линии, которые, стремясь сократить свою длину и будучи «нагружены» частицами П., в частности массивными ионами, колеблются подобно натянутым струнам. Быстрая магнитозвуковая волна в области малых частот по существу лишь поляризацией отличается от альфвеновской (их скорости близки и определяются магнитным полем и инерцией тяжёлых ионов). В области же больших частот, где ионы можно считать неподвижными, она определяется инерцией электронов и имеет специфическую винтовую поляризацию. Поэтому здесь её называют «геликонной ветвью» колебаний, или «ветвью вистлеров», т. е. свистов, поскольку в магнитосферной П. она проявляется в виде характерных свистов при радиосвязи. Кроме того, в П. может распространяться медленная магнитозвуковая волна, которая представляет собой обычную звуковую волну с характеристиками, несколько измененными магнитным полем.

Т. о., при наличии магнитного поля в однородной П. возможны волны шести типов: три высокочастотные и три низкочастотные. Если температура или плотность П. в магнитном поле неоднородны, то возможны ещё так называемые «дрейфовые» волны. При больших амплитудах возможны «бесстолкновительные» ударные волны (наблюдаемые на границе магнитосферы), уединённые волны (солитоны), а также ряд др. «нелинейных» волн и, наконец, сильноразвитая турбулентность движения П.

В неравновесной П. при определённых условиях возможна «раскачка неустойчивостей», т. е. нарастание какого-либо из перечисленных типов волн до некоторого уровня насыщения. Возможны и более сложные случаи индуцированного возбуждения волн одного типа за счёт энергии волн другого типа.