БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Лит. см. при ст. Память.

Повтори'тель,электронный усилительный каскад с коэффициентом усиления ~1 (как правило, 0,95—0,99). П. широко применяют в разнообразных радиоэлектронных устройствах в качестве буферного каскада (т. н. трансформатора полного сопротивления), разделяющего резко отличающиеся по электрическому сопротивлению источник сигнала и его нагрузку. Различают П. напряжения и П. тока, инвертирующие и неинвертирующие П. (под инверсией понимают изменение полярности или фазы колебаний входного сигнала на выходе каскада). Общее свойство усилительного каскада — усиление мощности — сохраняется и в П., поэтому П. напряжения усиливает входной ток, а П. тока — входное напряжение.

Наиболее распространены неинвертирующие П. напряжения, для которых, в отличие от обычных усилительных каскадов, характерны повышенное входное полное сопротивление (в частности, меньшая входная ёмкость) и пониженное выходное полное сопротивление. Благодаря этой особенности П. может передавать сигнал от высокоомного источника (например, с полным сопротивлением ~ 1 Мом ) к низкоомной нагрузке (например, с полным сопротивлением ~ 10 ом ) практически без ослабления. Типичным примером низкоомной нагрузки может служить отрезок коаксиального кабеля, соединяющий отдельные блоки электронной аппаратуры.

В зависимости от типа электронного прибора, используемого в П. напряжения, различают катодный П. — на электронной лампе ( рис. , а), эмиттерный — на биполярном транзисторе ( рис. , б) и истоковый — на полевом транзисторе ( рис. , б). Все эти П. имеют глубокую («стопроцентную») отрицательную обратную связь и, в соответствии с её общими свойствами, повышенные линейность и стабильность характеристик, расширенные полосу пропускания частот и диапазон амплитуд входного сигнала. П. напряжения в интегральном исполнении осуществляют, как правило, на основе сдвоенного, или составного, транзистора.

Лит.: Эрглис К. Э., Степаненко И. П., Электронные усилители, 2 изд.,. М., 1964; Степаненко И. П., Основы теории транзисторов и транзисторных схем, 3 изд., М., 1973.

И. П. Степаненко.

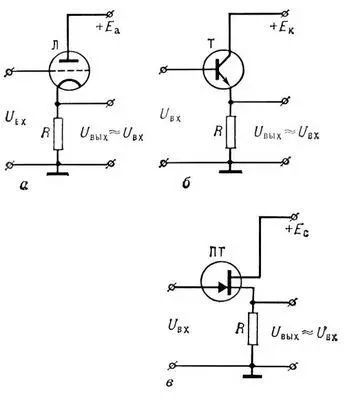
Повторители: а — катодный; б — эмиттерный; в — истоковый; Л — электронная лампа; Т — транзистор; ПТ — полевой транзистор; R — нагрузочный резистор; U вх— напряжение входного сигнала; U вых— напряжение выходного сигнала; Е а, E k, E c— постоянные напряжения, подаваемые соответственно на анод, коллектор и сток.

Повто'рного логари'фма зако'н,одна из предельных теорем теории вероятностей, близкая по смыслу к закону больших чисел (см. Больших чисел закон ) . П. л. з. указывает при определённых условиях точный порядок роста сумм независимых случайных величин при увеличении числа слагаемых. Пусть, например, случайные величины X 1, X 2,..., X n,... независимы и каждая из них принимает два значения: +1 или —1, каждое с вероятностью, равной 1/ 2, и пусть s n = X 1 + ... + X n. Тогда с вероятностью, равной 1, при любом d > 0:

1) при всех n, бо'льших некоторого (зависящего от случая) номера N:

s n< (1 + d)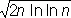

2) для бесконечной последовательности номеров n:

s n> (1 - d) .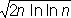

Название «П. л. з.» объясняется наличием в вышеприведённых выражениях множителя In In n. П. л. з. возник из задач т. н. метрической теории чисел (см. Чисел теория ) . Первый результат, относящийся к П. л. з., был установлен в 1924 А. Я. Хинчиным. Дальнейшие существенные продвижения в изучении условий приложимости П. л. з. связаны с работами А. Н. Колмогорова (1929) и В. Феллера (1943).

Лит.: Феллер В., Введение в теорию вероятностей и её приложения, пер. с англ., 2 изд., т. 1, М., 1967.

Ю. В. Прохоров.

Повто'рные посе'вы,1) вторичные посевы с.-х. растений на поле после уборки урожая основной культуры, дают урожай в этом же году. Позволяют производительнее использовать землю и получать больше сельскохозяйственной продукции с единицы площади. Распространены в достаточно увлажнённых районах с продолжительной тёплой осенью и в орошаемом земледелии. В Средней Азии, Закавказье, на Северном Кавказе и Ю. Украины применяют пожнивные посевы (например, после уборки озимого ячменя участки засевают др. зерновой культурой — гречихой, просом, ранней кукурузой, горохом) и получают 2-й урожай (зерно или зелёную массу). Там же и в более северных районах используют поукосные посевы — после снятия 1-й культуры до физиологической спелости (например, озимую рожь на зелёный корм) выращивают кормовую капусту, турнепс.

2) Посевы одной и той же культуры на одном поле 2 или несколько лет подряд. Распространены в зонах, специализирующихся на выращивании хлопчатника, риса, пшеницы и др., которые в условиях достаточного удобрения и увлажнения не снижают урожая при повторном выращивании. Применяют также на запольных участках (не входящих в севооборот), например выращивание конопли 2—3 года подряд на хорошо удобренном навозом коноплянике. См. также Монокультура.

Лит.: Два урожая кормовых культур в год, М., 1968; Земледелие, под ред. С. А. Воробьева, 2 изд., М., 1972.

С. А. Воробьев.

Повто'рный интегра'л,понятие интегрального исчисления. Вычисление двойного интеграла

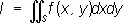
(см. Кратный интеграл ) от функции f ( x, у ) по области S, ограниченной прямыми х = а, х = b и кривыми y = j 1 ( x ) , у = j 2 ( х ) , при некоторых условиях относительно функций f ( x, у ) , j 1 ( x ) , j 2 ( х ) , производится по формуле:

,

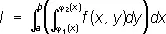где при вычислении внутреннего интеграла х считается постоянным. Таким образом, вычисление двойного интеграла сводится к двум вычислениям обычных интегралов, или, как говорят, к П. и. Геометрически сведение двойного интеграла к П. и. означает возможность вычисления объёма цилиндроида как путём разбиения его на элементарные столбики, так и путём разбиения его на элементарные слои, параллельные плоскости yOz. При некоторых условиях на функцию f ( x, у ) область S в П. и. можно изменить порядок интегрирования (то есть сначала интегрировать по х, а потом по у ) . Аналогично определяется П. и. в случае функций большего числа переменных.