БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Наличие двух разноимённо заряженных типов носителей тока — электронов и дырок является общим свойством П. и диэлектриков. В идеальных кристаллах эти носители появляются всегда парами — возбуждение одного из связанных электронов и превращение его в электрон проводимости неизбежно вызывает появление дырки, так что концентрации обоих типов носителей равны. Это не означает, что вклад их в электропроводность одинаков, т.к. скорость перехода из ячейки в ячейку (подвижность) у электронов и дырок может быть различной (см. ниже). В реальных кристаллах, содержащих примеси и дефекты структуры, равенство концентраций электронов и дырок может нарушаться, так что электропроводность осуществляется практически только одним типом носителей (см. ниже).

Зонная структура полупроводников.Полное и строгое описание природы носителей тока в П. и законов их движения даётся в рамках квантовой теории твёрдого тела, основные результаты которой могут быть сформулированы следующим образом:

а) В кристаллах энергетический спектр электронов состоит из интервалов энергий, сплошь заполненных уровнями энергии (разрешенные зоны) и разделённых друг от друга интервалами, в которых электронных уровней нет (запрещённые зоны) ( рис. 1 ).

б) Различные состояния электрона в пределах каждой зоны характеризуются, помимо энергии, квазиимпульсом р , принимающим любые значения в пределах некоторых ограниченных областей в импульсном пространстве ( р -пространстве), называются зонами Бриллюэна. Форма и размеры зоны Бриллюэна определяются симметрией кристалла и его межатомными расстояниями d. Величина р макс £ h/d, где h — Планка постоянная. Уравнение движения электрона проводимости в кристалле похоже на уравнение движения электрона в вакууме с той, однако, существенной разницей, что соотношения E = р 2/m 0 и u p = p/m 0 ( m 0— масса свободного электрона, E — его энергия, р — импульс, u — скорость) заменяются более сложной и индивидуальной для каждого кристалла и каждой его энергетической зоны зависимостью E ( p ): u p = .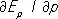

в) При абсолютном нуле температуры электроны заполняют наинизшие уровни энергии. В силу Паули принципа в каждом состоянии, характеризующемся определённой энергией, квазиимпульсом и одной из двух возможных ориентаций спина, может находиться только один электрон. Поэтому в зависимости от концентрации электронов в кристалле они заполняют несколько наинизших разрешенных зон, оставляя более высоко лежащие зоны пустыми. Кристалл, у которого при Т = 0 К часть нижних зон целиком заполнена, а более высокие зоны пусты, является диэлектриком или П. ( рис. 1 , а), металл возникает лишь в том случае, если хотя бы одна из разрешенных зон уже при Т = 0 К заполнена частично ( рис. 1 , б).

В П. и диэлектриках верхние из заполненных разрешенных зон называются валентными, а наиболее низкие из незаполненных — зонами проводимости. При Т > 0 К тепловое движение «выбрасывает» часть электронов из валентной зоны в зону проводимости (т. е. разрушает часть химических связей; см. выше). В валентной зоне при этом появляются дырки ( рис. 2 ).

Носители тока в П. сосредоточены, как правило, в довольно узких областях энергий: электроны — вблизи нижнего края (дна) зоны проводимости E c , на энергетических расстояниях ~ kT от неё ( kT — энергия теплового движения); дырки — в области такой же ширины вблизи верхнего края (потолка) валентной зоны E u. Даже при самых высоких температурах (~ 1000°) kT ~ 0,1 эв, а ширина разрешенных зон обычно порядка 1—10 эв. В этих узких областях ~kT сложные зависимости E ( p ), как правило, принимают более простой вид. Например, для электронов вблизи дна зоны проводимости:

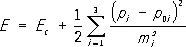
Здесь индекс i нумерует оси координат, p 0i— квазиимпульсы, соответствующие E c в зоне проводимости или E u в валентной зоне. Коэффициенты m э i называются эффективными массами электронов проводимости. Они входят в уравнение движения электрона проводимости подобно m 0 в уравнении движения свободного электрона. Всё сказанное справедливо для дырок валентной зоны, где

.

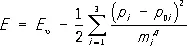Эффективные массы электронов m э и дырок m дне совпадают с m 0 и, как правило, анизотропны. Поэтому в разных условиях один и тот же носитель ведёт себя как частица с разными эффективными массами. Например, в электрическом поле Е, направленном вдоль оси oz, он ускоряется, как частица с зарядом е и массой m э z, а в магнитном поле H, направленном вдоль oz, движется по эллипсу в плоскости ^ Н с циклотронной частотой:

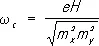
С квантовой точки зрения такое циклическое движение электронов и дырок в кристалле с частотой w созначает наличие уровней энергии (так называемых уровней Ландау), отстоящих друг от друга на 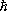w с. Значения эффективных масс электронов и дырок в разных П. варьируются от сотых долей m 0 до сотен m 0.

Ширина запрещенной зоны D E (минимальная энергия, отделяющая заполненную зону от пустой) также колеблется в широких пределах. Так, при Т ® 0 К D E = 0,165 эв в PbSe, 0,22 эв в InSb, 0,33 эв в Te, 0,745 эв в Ge, 1,17 эв в Si, 1,51 эв в GaAs, 2,32 эв в GaP, 2,58 эв в CdS, 5,6 эв в алмазе, а серое олово является примером П., у которого D E = 0, т. е. верхний край валентной зоны точно совпадает с нижним краем зоны проводимости ( полуметалл ) . Более сложные соединения и сплавы П., близких по структуре, позволяют найти П. с любым D E от 0 до 2—3 эв.

Зонная структура наиболее полно изучена для алмазоподобных П., в первую очередь Ge, Si и соединений A IIIB V; многое известно для Te, соединений A IVB VIи др. Весьма типичной является зонная структура Ge ( рис. 3 ), у которого вблизи своего верхнего края соприкасаются две валентные зоны. Это означает существование двух типов дырок — тяжёлых и легких с эффективными массами 0,3 m 0 и 0,04 m 0 . На 0,3 эв ниже расположена ещё одна валентная зона, в которую, однако, как правило, дырки уже не попадают. Для зоны проводимости Ge характерно наличие трёх типов минимумов функции E ( р ) : L, Г и D. Наинизший из них — L -минимум, расположенный на границе зоны Бриллюэна в направлении кристаллографической оси [111]. Расстояние его от верхнего края валентной зоны и есть ширина запрещенной зоны D E = 0,74 эв (при температурах, близких к абсолютному нулю; с ростом температуры D E несколько уменьшается). Эффективные массы вблизи L -минимума сильно анизотропны: 1,6 m 0для движения вдоль направления [111] и 0,08 m 0для перпендикулярных направлений. Четырём эквивалентным направлениям [111] (диагонали куба) в кристалле Ge соответствуют 4 эквивалентных L -минимума. Минимумы Г и Д расположены соответственно при р = 0 и в направлении оси [100], по энергии выше L -минимума на 0,15 эв и 0,2 эв . Поэтому количество электронов проводимости в них, как правило, гораздо меньше, чем в L -минимуме.