БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Совокупная характеристика размеров и количества П. в теле, т. е. занимаемого П. суммарного пространства, называется пористостью. Её выражают объёмом П. в единице объёма или массы пористого тела, а также его поверхностью удельной. Искусственные и природные пористые тела широко используются в технике; пористость горных пород и почв определяет интенсивность и характер многих процессов, связанных с тепло- и массо-обменом в земной коре и на её поверхности.

Лит.: Грег С., Синг К., Адсорбция, удельная поверхность, пористость, пер. с англ., М., 1970; Dubinin М. М., Porous structure and adsorption properties of active carbons, в кн.: Chemistry and physics of carbon, v. 2, N. Y., 1966, p. 51.

Л. А. Шиц.

Поря'дковые чи'сла, ординальные числа, понятие множеств теории; см. Трансфинитные числа, Число.

Поря'дковый но'мер, номер места, занимаемого химическим элементом в периодической системе элементов Д. И. Менделеева; то же, что атомный номер элемента.

Поря'дная за'пись(от слова «ряд» — договор, сделка), документ, оформлявший на Руси различного рода договоры. В 16—17 вв. П. з. заключались на житьё крестьян, дворников, церковных дьячков, на выучку подмастерьев ремеслу, наём земли, на строительные (возведение городских стен, церквей и пр.) и т.п. П. з. — важный источник по истории экономической жизни и социальных отношений 16—17 вв. Особо велико историческое значение крестьянских П. з. В них оговаривалось предоставление землевладельцем новопорядчику участка земли, «подмоги» (инвентарь, скот, семена или деньги) на обзаведение хозяйством и временного освобождения его от государственных податей и феодальных повинностей. Во избежание невыполнения новопорядчиком взятых на себя обязательств и для удержания его на новом месте в П. з. в некоторых случаях оговаривалась уплата им неустойки, обычно значительно превышавшей «подмогу».

Поря'док(ordo), одна из основных категорий систематики, объединяющая родственные семейства растений. Например, семейства вязовые, тутовые, коноплёвые и крапивные образуют П. крапивоцветных (Urticales). Латинское название П. обычно образуют, прибавляя окончание -ales к основе названия семейства. П. часто объединяет 2—3 и более (до 20) семейств, иногда включает всего 1 семейство (например, П. ивоцветных Salicales с единственным семейством Salicaceae). Крупные П. иногда разделяют на подпорядки (subordo). Число П. в различных филогенетических системах неодинаково (по одной системе, все семейства цветковых растений объединяют в 94 П., по другой — в 78 П.). Родственные П. объединяют в классы; при этом промежуточными категориями могут быть надпорядок и подкласс. В систематике животных П. соответствует отряд.

Поря'док интерфере'нции, разность хода интерферирующих лучей света, деленная на длину их волны (см. Интерференция света ) . Чаще всего рассматривают П. и., равные целым числам (длин волн): 0 ± 1, ± 2..., т.к. именно в этих случаях наиболее сильно проявляется эффект интерференции. Если лучи на своём пути отражаются от какой-либо поверхности, в П. и. включается происходящий при этом сдвиг фазы (скачок фазы), деленный на 2l (см. Отражение света ) .

Поря'док(математический), числовая характеристика математических объектов.

1) П. алгебраической кривой F ( х, у ) = 0, где F ( х, у ) — многочлен от х и y, называют наивысшую степень членов этого многочлена. Например, эллипс 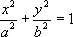есть кривая второго П., а лемниската ( х 2 + у 2 ) 2 = а 2 ( х 2— у 2 ) — кривая четвёртого П.

2) П. бесконечно малой величины a относительно бесконечно малой величины b — такое число n, что существует конечный предел 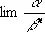отличный от нуля. Например, sin 23 х при х ® 0 есть бесконечно малая второго П. относительно х, так как 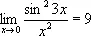. Вообще говорят, что a — бесконечно малая высшего П., чем b, если 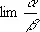и низшего П., чем b, если 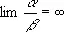. Аналогично определяют П. бесконечно больших величин.

3) П. нуля (соответственно полюса) а функции f ( x ) — такое число n, что существует конечный 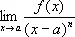[соответственно lim ( х — a ) nf (x)], отличный от нуля (см. Нуль функции ) .

4) П. производной — число дифференцирований, которые надо произвести над функцией, чтобы получить эту производную (см. Дифференциальное исчисление ) . Например , у''' — производная третьего П., 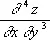— производная четвёртого П. Аналогично определяют П. дифференциала.

5) П. дифференциального уравнения — наивысший из П. производных, входящих в уравнение. Например, у’’’ у’ — ( y’’ ) 2 = 1 — уравнение третьего П., у’’ — 3 у’ + у = 0 — уравнение второго П.

6) П. квадратной матрицы— число её строк или столбцов.

7) П. конечной группы— число элементов группы. П. элемента а группы — наименьший положительный показатель n степени a n , равной единице группы; если такого n нет, то а называют элементом бесконечного П.

8) Если при некотором исследовании или вычислении отбрасываются все степени некоторой малой величины, начиная с ( n + 1)-й, то говорят, что исследование или вычисление ведётся с точностью до величин n -го П. Например, при исследовании малых колебаний струны пренебрегают величинами, содержащими вторые и высшие степени прогиба и его производных, получая благодаря этому линейное уравнение (линеаризируя задачу).

9) Слово «П.» употребляется также в исчислении конечных разностей (разности различных П.), в теории многих специальных функций (например, цилиндрические функции n- го П.) и т.д.

10) При измерениях говорят о величине порядка 10 n, подразумевая под этим, что она заключена между 0,5×10 nи 5×10 n.

Поря'док реа'кции, понятие кинетики химической. П. р. определяется как сумма показателей степеней n 1 и n 2 в уравнении

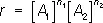, (1)