БСЭ БСЭ - Большая Советская Энциклопедия (ПУ)

Как точное П. р. появляется в теории случайных процессов. Например, при расчёте нагрузки линий связи обычно предполагают, что количества вызовов, поступивших за непересекающиеся интервалы времени, суть независимые случайные величины, подчиняющиеся П. р. с параметрами, значения которых пропорциональны длинам соответствующих интервалов времени (см. Пуассоновский процесс ).

В качестве оценки неизвестного параметра l по n наблюдённым значениям независимых случайных величин X 1,..., X nиспользуется их арифметическое среднее X = ( X 1+ ... + X n)/ n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально (см. Статистические оценки ).

Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М. — Л., 1969; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.

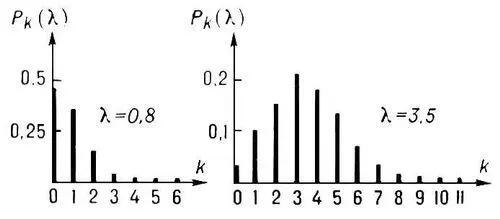
Рис. к ст. Пуассона распределение.

Пуассо'на теоре'ма,1) теорема теории вероятностей, описывающая поведение частоты появления некоторого события в последовательности независимых испытаний — частный случай закона больших чисел (точную формулировку см. в ст. Больших чисел закон ). 2) Одна из предельных теорем теории вероятностей. П. т. позволяет приближённо оценивать вероятность данного числа появлений маловероятного события при большом числе независимых испытаний (см. Пуассона распределение ).

Обе теоремы установлены С. Д. Пуассоном в 1837.

Пуассо'на уравне'ние,уравнение с частными производными вида D u = f, где D —оператор Лапласа:

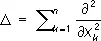
При n = 3 этому уравнению удовлетворяет потенциалu ( х, у, z ) объёмных масс, распределённых с плотностью f ( x, у, z )/4p (в областях, где f = 0 потенциал u удовлетворяет уравнению Лапласа), а также потенциал объёмно распределённых электрических зарядов. При этом плотность распределения f должна удовлетворять известным требованиям гладкости (например, условию непрерывности частных производных). Если функция f отлична от нуля лишь в конечной области G, ограничена и имеет непрерывные частные производные первого порядка, то при n = 2 частное решение П. у. имеет вид:

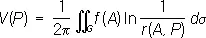
а при n = 3:

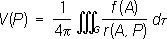
где r ( А , Р ) — расстояние между переменной точкой интегрирования А и некоторой точкой Р . В более подробной записи

V ( х, у, z ) =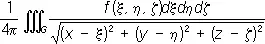

Решение краевых задач для П. у. сводится подстановкой 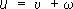к решению краевых задач для уравнения Лапласа Dw = 0.

П. у. впервые (1812) было изучено С. Д. Пуассоном.

Пуассо'на фо'рмула сумми'рования,формула для вычисления суммы ряда вида

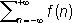
Если

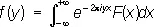
— Фурье преобразование (несколько иначе, чем обычно, нормированное) функции F ( x ), то

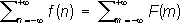
( m и n — целые). Это и есть П. ф. с.; она может быть записана в более общем виде: если l > 0, m > 0, lm = 1 и 0 £ t < 1 , то

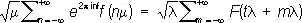
Для справедливости этой формулы достаточно, чтобы в каждом конечном интервале F ( x ) имела ограниченную вариацию, и для х ® + ¥ и х ® — ¥ выполнялось одно из условий: 1) F ( x ) — монотонна и абсолютно интегрируема; 2) F ( x ) — интегрируема и обладает абсолютно интегрируемой производной. П. ф. с. позволяет в ряде случаев заменить вычисление суммы ряда вычислением суммы др. ряда, сходящегося быстрее первоначального.

Пуассо'новский пото'к,то же, что пуассоновский процесс. Этот термин используют, как правило, в массового обслуживания теории.

Пуассо'новский проце'сс,случайный процесс, описывающий моменты наступления 0 < t 1<...< t n<...<... каких-либо случайных событий, в котором число событий, происходящих в течение любого фиксированного интервала времени, имеет Пуассона распределение и независимы числа событий, происходящих в непересекающиеся промежутки времени.

Пусть m( s , t ) — число событий, моменты наступления которых t iудовлетворяют неравенствам 0 £ s < t i£ t , и пусть l( s, t ) — математическое ожидание m( s , t ) . Тогда и П. п. при любых 0 £ s 1 < t 1 £ s 2 < t 2£... £ s r< t rслучайные величины m( s 1, t 1), m( s 2, t 2),... m( s r, t r) независимы и вероятность того, что m(s, t ) = n, равна

e - l (s, t)[l( s, t )] n/ n !.

В однородном П. п. l( s, t ) = a ( t — s ) , где а — среднее число событий в единицу времени, расстояния t n — t n-1 между соседними моментами t nнезависимы и имеют показательное распределение с плотностью ae -at, t ³ 0.

Если имеется много независимых процессов, описывающих моменты возникновения некоторых случайных редких событий, то суммарный процесс при определённых условиях в пределе даёт П. п.

П. п. представляет собой удобную математическую модель, которая часто используется в различных приложениях теории вероятностей. В частности, с помощью П. п. описывается поток требований (например, вызовов, поступающих на телефонную станцию, выездов медицинских машин скорой помощи при транспортных происшествиях в большом городе) в массового обслуживания теории.

Обобщением П. п. является пуассоновское случайное распределение точек на плоскости или в пространстве, при котором число точек в любой фиксированной области имеет распределение Пуассона (со средним, пропорциональным площади или объёму области) и числа точек в непересекающихся областях независимы. Это распределение часто используется при расчётах в астрономии, физике, экологии, технике и т.д.