БСЭ БСЭ - Большая Советская Энциклопедия (РА)

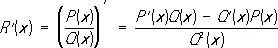
также является Р. ф. Интеграл от Р. ф. сводится по предыдущему к сумме интеграла от многочлена и интеграла от правильной Р. ф. Интеграл от многочлена является многочленом и его вычисление не представляет труда. Для вычисления второго интеграла пользуются формулой разложения правильной Р. ф. R 1( x ) на простейшие дроби:

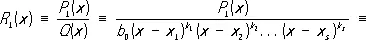
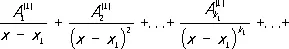
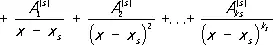
где x 1, ..., x s — различные корни многочлена Q ( x ) соответственно кратностей k 1, ..., k s ( k 1+ ... + k s = m ), a 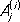— постоянные коэффициенты. Разложение Р. ф. на простейшие дроби (2) определяется однозначно. Если коэффициенты многочленов P 1( x ) и Q ( x ) — действительные числа, то комплексные корни знаменателя Q ( x ) (в случае их существования) распадаются на пары сопряжённых, и соответствующие каждой такой паре простейшие дроби в разложении (2) могут быть объединены в вещественные простейшие дроби:

где трёхчлен x 2+ px + q имеет комплексно-сопряжённые корни (4 q > p 2).

Для определения коэффициентов 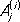, B j и D j можно воспользоваться неопределенных коэффициентов методом. Интегралы от простейших дробе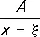й

и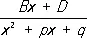

не являются Р. ф

,

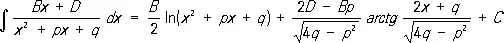
а интегралы от простейших дробе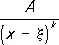й

и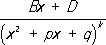

при k > 1 являются: первый — Р. ф., а второй — суммой Р. ф. и интеграла такого же вида, как при k = 1. Т. о., интеграл от любой Р. ф. (не являющейся многочленом) представляется в виде суммы Р. ф., арктангенсов и логарифмических функций. М. В. Остроградский дал алгебраический метод определения рациональной части интеграла от Р. ф., не требующий ни разложения Р. ф. на простейшие дроби, ни интегрирования (см. Остроградского метод ).

Р. ф. являются весьма важным классом элементарных функций. Рассматриваются также Р. ф. нескольких переменных; они получаются в результате конечного числа арифметических операций над их аргументами и произвольными числами. Так,

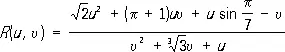
даёт пример Р. ф. двух переменных u и u .

В середине 20 в. Р. ф. нашли широкое применение в вопросах приближения функций (см. Приближение и интерполирование функций ).

Рациона'льное выраже'ние,алгебраическое выражение, не содержащее радикалов, например a 2+ b , х /( у — z 3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию от этих переменных.

Рациона'льное число',число, которое может быть представлено в виде дроби , где m и n — целые числа ( n ¹ 0). Т. к. целое число m можно представить в виде 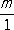, то все целые являются Р. ч. В области Р. ч. действия сложения, вычитания, умножения и деления (на делитель, отличный от нуля) всегда выполнимы; т. о., Р. ч. образуют поле (см. Поле алгебраическое). Основные правила действий над Р. ч. даются формулами:

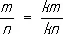( k ¹ 0); ; ; .

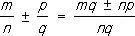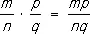Р. ч. могут быть также представлены конечными десятичными или бесконечными периодическими дробями. Всякое иррациональное число может быть заключено между двумя Р. ч. (значениями по недостатку и по избытку), разность между которыми сколь угодно мала.

Рациона'льные но'рмы потребле'ния,см. Нормы потребления.

Ра'чинский хребе'т,горный хребет в южной части Большого Кавказа, в Грузинской ССР. Высота до 2862 м. Сложен главным образом известняками, порфиритами и туфогенными сланцами. Широко развит карст (Шаорская котловина — карстовое полье, превращенное в водохранилище). На склонах широколиственные леса (главным образом из бука), темнохвойные леса, субальпийские и альпийские луга. У юго-западных отрогов — Ткибульское месторождение угля.

Ра'чинцы,этнографическая группа грузин. Живут главным образом в бассейне верховьев р. Риони (в Амбролаурском и Онском районах Грузинской ССР). Говорят на рачинском диалекте грузинского языка. В прошлом отличались местными особенностями культуры и быта. Были известны как искусные домостроители.

Ра'чич(Račić) Йосип (22.3.1885, Хорвати, близ Загреба, — 20.6.1908, Париж), хорватский живописец и график. Один из создателей хорватской школы живописи 20 в. Учился в Мюнхене в школе А. Ажбе и АХ (1905—08). Автор портретов и жанровых композиций, отличающихся непринуждённой интимностью образов, драматической выразительностью обобщённой манеры и сдержанной, размытой, богатой тоновыми переходами цветовой гаммы (автопортрет, «Дама в чёрном», 1907, «Мать и дитя», 1908, — все в Современной галерее, Загреб), а также рисунков углем, карандашом, акварелью.

Лит.: J. Račić. [Katalog izložbe], Zagreb, 1961.

Й. Рачич. Автопортрет. Современная галерея. Загреб.