БСЭ БСЭ - Большая Советская Энциклопедия (СА)

Д. Н. Зубарев.

Самосозна'ние,осознание, оценка человеком своего знания, нравственного облика и интересов, идеалов и мотивов поведения, целостная оценка самого себя как деятеля, как чувствующего и мыслящего существа. С. свойственно не только индивиду, но и обществу, классу, социальной группе, когда они поднимаются до понимания своего положения в системе производственных отношений, своих общих интересов и идеалов. В С. человек выделяет себя из всего окружающего мира, определяет своё место в круговороте природных и общественных событий. С. тесно связано с рефлексией , где оно поднимается на уровень теоретического мышления. С. формируется на определённой ступени развития личности под влиянием образа жизни , который требует от человека самоконтроля собственных поступков и действий, принятия полной ответственности за них.

Поскольку мерой и исходным пунктом отношения человека к себе выступают прежде всего другие люди, С. по самому существу носит глубоко общественный характер. См. ст. Сознание и литературу при ней.

А. Г. Спиркин.

Самосопряжённая ма'трица(математическая), матрица , совпадающая со своей сопряжённой, т. е. такая, что a ik = 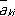, где — число, комплексно сопряжённое с а. Если элементы С. м. действительны, то она симметрическая (см. Симметрическая матрица ) . С. м. имеет действительные собственные значения l 1, l 2,..., l n и соответствует линейному преобразованию в комплексном n -мерном пространстве, сводящемуся к растяжениям в |l i| раз по n взаимно перпендикулярным направлениям и зеркальным отражениям в плоскостях, ортогональных тем из этих направлений, для которых l i < 0. Билинейную форму вида 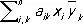, коэффициенты которой образуют С. м., называют эрмитовой формой. Всякая матрица может быть записана в виде A 1+ iA 2 , где A 1и A 2 суть С. м., а также в виде AU, где А является С. м., a U — унитарная матрица. Если А и В суть С. м., то AB является С. м. тогда и только тогда, когда А и В перестановочны.

Самосопряжённое дифференциа'льное уравне'ние,уравнение, имеющее те же решения, что и сопряжённое с ним (см. Сопряжённые дифференциальные уравнения ) . Обыкновенное С. д. у. чётного порядка 2 m имеет вид

,

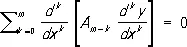а нечётного порядка 2 m — 1 имеет вид

,

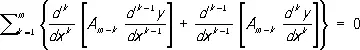где A i — функции от x. Понятие С. д. у. играет большую роль в теории дифференциальных уравнений, обыкновенных и с частными производными. При некоторых краевых условиях левая часть С. д. у. определяет самосопряжённый дифференциальный оператор. Наиболее важны в приложениях С. д. у. второго порядка.

Самосопряжённый опера'тороператор, совпадающий со своим сопряжённым (см. Сопряжённые операторы ) . иначе называется эрмитовым. Теория С. о. возникла как обобщение теории интегральных уравнений с симметричным ядром, самосопряжённых дифференциальных уравнений, симметрических матриц и т. д. Примерами С. о. могут служить оператор умножения на независимое переменное в пространстве функций, заданных на всей числовой прямой и имеющих интегрируемый квадрат, оператор дифференцирования 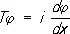в том же пространстве и т. д.

Если функция К ( х, у ) непрерывна на квадрате а £ х £ b, а £ у £ b и К ( х, у ) = К ( у, х ) , то интегральный оператор 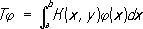самосопряжён. Спектр С. о. (см. Спектр оператора ) лежит на действительной оси. В квантовой механике физическим величинам соответствуют С. о., спектр которых даёт возможные значения этих величин. С. о. может быть в известном смысле представлен в виде интеграла, являющегося пределом линейных комбинаций попарно ортогональных проекционных операторов с действительными коэффициентами. См. Спектральный анализ линейных операторов, Операторов теория .

Самостери'льность,неспособность растений к образованию семян при самоопылении .

Самостоя'тельный бала'нс,отчётный документ производственных предприятий и объединений, организаций и учреждений в СССР, ведущих законченный бухгалтерский учёт. Хозрасчётные предприятия осуществляют учёт и составляют С. б. отдельно по основной деятельности, капитальным вложениям и рабочему снабжению. Всесоюзные и республиканские промышленные объединения составляют сводные отчёты и балансы по всем видам производственно-хозяйственной деятельности. Выделение отдельных отраслей деятельности предприятий (подсобное сельское хозяйство, лесозаготовки, жилищно-коммунальное хозяйство и др.) на С. б. усиливает контроль за целевым использованием средств. Предприятия и их части, находящиеся на С. б., имеют свой расчётный счёт в банке, вступают в хозяйственно-правовые и расчётные отношения с другими предприятиями, организациями и учреждениями.

Самостя'гивающийся разря'д,электрический разряд в газе, сечение токового канала которого уменьшается под действием порождаемого им самим («собственного») магнитного поля. Подробнее см. Пинч-эффект .

Самосу'д,самочинная расправа над действительным или мнимым преступником, сопровождающаяся, как правило, мучительством. В Западной Европе в средние века существовал в различных формах: как легализованное самочинное действие, допускавшееся при отказе в судебной защите притязания (так называемое кулачное право ), как суд фемов — орудие скорой и беспощадной расправы с крестьянством. Нередко С. являлся следствием религиозного фанатизма, разжигаемого искусно поддерживаемой церковью верой в колдовство (ритуальные убийства и пр.).

В современных буржуазных государствах сохранились некоторые формы С.: «Линча суд» (в США), взрывы бомб в общественных местах, организация катастроф на транспорте и т. и.