БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

Сингёнхянпха'(школа нового направления), направление корейской демократической литературы в 20-е гг. 20 в. Связано с деятельностью молодых писателей (На До Хян, Чо Мен Хи, Цой Со Хэ, Ли Ги Ён, Ли Ик Сан и др.), обратившихся к изображению низших слоев корейского общества. Для их реалистического творчества, несмотря на элементы излишней драматизации, характерна ярко выраженная патриотическая и социальная направленность. С. часто называют прологом к корейской пролетарской литературе.

Лит.: Иванова В. И., Из истории пролетарского литературного движения в Корее (1924 — 1934), «Краткие сообщения ИВ АН СССР», 1958, в. 24; Ли В. Н., Корейская ассоциация пролетарских писателей и проза 20—30-х гг., в сборнике: Национальные традиции и генезис социалистического реализма, М., 1965.

В. И. Иванова.

Сингиду'нум(лат. Singidunum), древнее кельтское поселение, затем римская крепость; была расположена на месте современного Белграда .

Синги'ль(Mugil auratus), рыба семейства кефалей . Распространена у берегов Западной Европы и Северо-Западной Африки (от Англии и Норвегии до Марокко), а также в Средиземном, Чёрном и Азовском морях; акклиматизирована в Каспийском м. Длина 20—40 см , иногда до 52 см . Быстрая стайная рыба, выпрыгивающая из воды при испуге. Зимует в море, нагуливается у берегов, заходит в лагуны и устья рек. Питается детритом и обрастаниями. Нерест осенью в открытом море; икра плавучая. Ценная промысловая рыба. Мальков выращивают в отгораживаемых от моря лагунах (кефальное хозяйство).

Рис. к ст. Сингиль.

Сингитико'с(Singitikós), Айон-Орос, залив Эгейского моря у южного берега полуострова Халкидики (Греция), между гористыми полуостровами Ситонья и Айон-Орос . Длина 50 км , ширина у входа около 25 км . Глубиной до 500 м . Приливы полусуточные, их величина менее 0,5 м .

Сингони'я кристаллографи'ческая,подразделение кристаллов по признаку симметрии их элементарной ячейки . С. к. характеризуется соотношениями между осями а , b , с и углами a, b, g ячейки. Существует 7 С. к.: кубическая ( а = b = с , a = b = g = 90°), тетрагональная ( а = b ¹ с , a = b = g = 90°), гексагональная ( а = b ¹ с , a = b = 90°, g = 120°), тригональная ( а = b = с , a = b = g ¹ 90°), ромбическая ( а ¹ b ¹ с , a = b = g = 90°), моноклинная ( а ¹ b ¹ с , a = g = 90°, b ¹ 90°), триклинная ( a ¹ b ¹ c , a ¹ b ¹ g ¹ 90°). Являясь наиболее крупным классификационным подразделением в симметрии кристаллов , каждая С. к. включает в себя несколько точечных групп симметрий и Браве решёток .

Лит.: Попов Г. М., Шафрановский И. И., Кристаллография, 5 изд., М., 1972.

Сингуля'рная ма'трица(от лат. singularis — отдельный, особый), то же, что особая матрица .

Сингуля'рная то'чка,точка на диаграмме состояния или на диаграмме состав — свойство, отвечающая образованию недиссоциированного соединения. Например, в системе из компонентов А и В образование такого соединения С выражается точкой D (см. Двойные системы , рис. 5 ). В точке D пересекаются две ветви линии ликвидуса (геометрического места температур начала кристаллизации), которые принадлежат одной и той же непрерывной кривой, отвечающей выделению из жидкости одной твёрдой фазы С , как этого требуют принципы непрерывности и соответствия (см. Физико-химический анализ ). С. т. наблюдаются на диаграммах состав — свойство жидких систем, а также твёрдых растворов, если в них происходят превращения с образованием определённых соединений — дальтонидов (см. Дальтониды и бертоллиды ).

Лит.: Курнаков Н. С., Избр. труды, т. 1—3, М., 1960—63; Аносов В. Я., Погодин С. А., Основные начала физико-химического анализа, М. — Л., 1947.

Сингуля'рные интегра'льные уравне'ния, интегральные уравнения с ядрами, обращающимися в бесконечность в области интегрирования так, что соответствующий несобственный интеграл, содержащий неизвестную функцию, расходится и заменяется своим главным значением по Коши. Примером С. и. у. может служить следующее уравнение с т. н. ядром Гильберта:

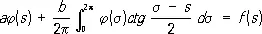
решением которого является функция

,

, ,

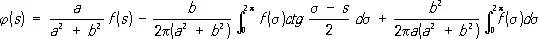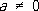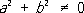где первый интеграл также понимается в смысле главного значения по Коши.

Хорошо изученным общим классом С. и. у. являются уравнения с ядром Коши вида:

, (*)

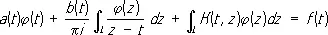где a ( t ), b ( t ), f ( t ) — заданные непрерывные функции точки t пути интегрирования L (который может состоять из конечного числа гладких самонепересекающихся замкнутых или незамкнутых кривых с непрерывной кривизной) в комплексной плоскости; сингулярный интеграл

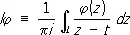
понимается как предел при e ® 0 интеграла 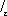j по пути L e, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро K ( t , z ) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К С. и. у. вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.

Исследование С. и. у. (*) опирается на свойства сингулярного интеграла I j, которые зависят от предположений, делаемых относительно j. Подробно С. и. у. исследованы в пространстве непрерывных функций j и в пространстве функций, интегрируемых с квадратом. Основное свойство сингулярного интеграла I j выражается равенством 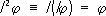, справедливым для широкого класса функций.