БСЭ БСЭ - Большая Советская Энциклопедия (СИ)

| p a | = | p b | = | p’ a | = | р’ b | (см. рис. 2 ).

Амплитуда рассеяния является функцией двух переменных: энергии системы Е и угла J, на который в результате рассеяния отклоняется одна из частиц. Эти переменные могут быть выражены через 2 независимые релятивистски инвариантные величины

s = ( p a + p b ) 2= ( p’ a + p’ b ) 2,

t = ( p’ a – p a ) 2= ( p’ b – p b ) 2.

В с. ц. и. величина s равна квадрату полной энергии системы: s = ( E a + E b ) 2, а величина t равна (с обратным знаком) квадрату переданного (трёхмерного) импульса, t = – ( p’ a – p a ) 2, и выражается через угол рассеяния J: t = – 2 p 2 (1 – cosJ), где р — импульс частиц в с. ц. и. Наряду с величинами s , t вводится третья релятивистски инвариантная величина и .

u = ( р’ b – p a ) 2= ( р’ b – p b ) 2, (6’)

которая в силу закона сохранения энергии-импульса связана с величинами s и t соотношением: s + t + u = 2 m a + 2 m b , где ma , m b — массы частиц «а» и «b». В процессах упругого рассеяния частиц область изменения величины s ограничена неравенством s ³ ( m a + m b ), а область изменения t — неравенствами 0 > t > -4 p 2 . Эту область изменения переменных называется физической областью. Амплитуда рассеяния при фиксированной передаче импульса t может быть продолжена в комплексную область по энергетической переменной s и оказывается связанной с амплитудой рассеяния античастиц . Эта связь заключается в следующем. Рассмотрим наряду с реакцией упругого рассеяния какого-либо частиц, например p ±-мезонов на протонах:

p +( p ) + р ( q ) ® p +( p' ) + р ( q' ) (I)

(в скобках указаны четырёхмерные импульсы частиц), реакцию рассеяния

p -(- р ) + р ( q ) ® p -(- p’ ) + р ( q ), (II)

получающуюся из (1) переносом символа p-мезона из одной части равенства в другую с одновременной заменой частицы (p +) на античастицу (p -) и знаков их четырёхмерных импульсов: р ® - р , p' ® - p' . При переходе от процесса (I) к процессу (II) переменная t остаётся неизменной, а s и и меняются местами. Физической области обоих процессов соответствуют двум различным неперекрывающимся областям изменения кинематических переменных s , и . Доказательство Боголюбовым аналитичности амплитуды в комплексной плоскости переменной s позволяет утверждать, что амплитуды процессов I и II являются предельными значениями единой аналитической функции Ft ( s ) в разных областях изменения переменной s с разрезами на вещественной оси ( рис. 4 ). Правый разрез определяется условием s ³ ( М + m)' (где М и m, — массы протона и пиона), а левый разрез — условием u = 2 M 2 + 2m 2- s - t ³ ( M + m 2). На «верхнем берегу» правого разреза Ft ( s ) совпадает с амплитудой T ( s , t ) процесса (I):

,

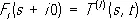а на «нижнем берегу» левого разреза — с амплитудой процесса (II):

.

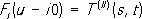Отсюда вытекает соотношение т. н. перекрёстной симметрии (или кроссинг-симметрии):

.

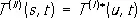Это соотношение связывает значение амплитуды одного процесса в его физической области со значением амплитуды др. процесса вне физической области последнего. Поэтому соотношение перекрёстной симметрии не имело бы смысла, если бы не существовало продолжения амплитуды процесса (1) из его физической области на левый разрез.

Для определения особых точек аналитической функции Ft ( s ) важнейшее значение имеет продолжение условия унитарности S -maтрицы в «нефизическую» область кинематических переменных (лежащую вне «физических» областей, определяемых законами сохранения энергии и импульса для начальных и конечных состояний). Так, если две частицы «а» и «b» могут переходить в результате С. в. в виртуальную частицу «с»: а + b ® с, то из условия унитарности следует, что амплитуда процесса рассеяния а + b ® а + b будет иметь полюс по переменной s при значении s = mc2 , где mc — масса частицы «с». Этот полюс при mc < ma + m b лежит в «нефизической» области процесса упругого рассеяния а + b ® а + b [«физическая» область, как уже отмечалось, начинается с s = ( m a + m b ) 2]. Если же mc > ma + m b , частица «с» нестабильна относительно распада (за счёт С. в.) с ® а + b, т. е. является резонансом, и полюс амплитуды расположен на «нефизическом» листе римановой поверхности, соответствующем аналитическому продолжению амплитуды через разрез в комплексной плоскости s (см. Аналитические функции ).

Тот факт, что особенности амплитуды, связанные с образованием виртуальных частиц, лежат в «нефизической» области, имеет простой смысл. Действительно, рождение виртуальных частиц сопровождается нарушением закона сохранения энергии, происходящим на короткое время в соответствии с соотношением неопределённостей. Поскольку физические области определяются законами сохранения энергии-импульса и условием стабильности начальных и конечных частиц в процессах С. в., образованию виртуальных состояний соответствуют значения кинематических переменных, лежащие вне этих областей. Т. о., именно в «нефизических» областях кинематических переменных содержится информация о процессах обмена виртуальными частицами, посредством которого и осуществляется С. в.

Помимо полюсов, амплитуда рассеяния может иметь и другие особые точки. Так, при энергии, соответствующей порогу к.-л. неупругого процесса, например а + b ® с + d [т. е. при s = ( mc + m d ) 2}, амплитуда реакции а + b ® а + b имеет точку ветвления. При ( mc + m d ) > ( ma + m b ) эти особенности лежат в физической области процесса а + b ® а + b и приводят к нерегулярностям в поведении эффективного сечения рассеяния частиц а + b вблизи порога рождения частиц с и d, вызванным появлением нового канала реакции.

Если предположить, что амплитуда рассеяния как функция переменных s , t , u имеет только те особые точки, которые возникают из обобщённого условия унитарности S -мaтрицы, то можно прийти к заключению, что единая аналитическая функция f ( s , u , t ) в разных областях изменения переменных описывает три различных процесса:

а + b ® с + d, (I)