БСЭ БСЭ - Большая Советская Энциклопедия (СО)

Лит.: Баптиданов Л. Н., Тарасов В. И., Электрооборудование электрических станций и подстанций, 3 изд., т. 1–2, М. — Л., 1959—60; Электротехнический справочник, 4 изд., т. 2, кн. 1, М., 1972.

Б. А. Князевский.

Со'бственные фу'нкции,понятие математического анализа. При решении многих задач математической физики (в теории колебаний, теплопроводности и т.д.) возникает необходимость в нахождении не равных тождественно нулю решений однородных линейных дифференциальных уравнений L ( y ) = l у , удовлетворяющих тем или иным краевым условиям. Такие решения называют С. ф. задачи, а соответствующие значения l — собственными значениями . Если дифференциальное уравнение с соответствующими краевыми условиями самосопряжённое (см. Самосопряжённое дифференциальное уравнение ), то его собственные значения действительны, а С. ф., соответствующие различным собственным значениям, ортогональны. Если дифференциальное уравнение рассматривается на конечном отрезке и его коэффициенты не имеют на этом отрезке особенностей, то множество С. ф. счётно (задача имеет дискретный спектр); знание С. ф. и соответствующих собственных значений позволяет тогда при некоторых условиях получить решение задачи в виде ряда по С. ф. (см. Фурье метод ). Если же уравнение рассматривается на бесконечном промежутке или его коэффициенты имеют особенности (например, если коэффициент при старшей производной обращается в нуль), может существовать континуум С. ф., и вместо разложения в ряд получается разложение в интеграл по С. ф., аналогичное представлению в виде Фурье интеграла . В этом случае говорят, что задача имеет непрерывный спектр. Многие специальные функции ( ортогональные многочлены и др.) служат С. ф. некоторых уравнений.

В теории интегральных уравнений С. ф. ядра К ( х , у ) называют функцию, удовлетворяющую при некотором значении l уравнению

.

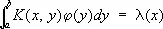Всякое симметрическое непрерывное ядро имеет С. ф. В этом случае всякая функция, представимая в виде

,

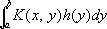может быть разложена в ряд по С. ф. Если ядро имеет особенности или задано в бесконечной области, то может также возникнуть непрерывный спектр.

Наиболее общим образом С. ф. можно определить как собственные векторы линейных операторов в линейных функциональных пространствах. В квантовой механике С. ф. оператора, отвечающего какой-либо физической величине (см. Операторы в квантовой теории), соответствуют состояниям системы, в которых данная физическая величина имеет определённое значение.

Иногда С. ф. называют также фундаментальными функциями, характеристическими функциями и т.д.

Со'буль(Soboul) Мариус Альбер (р. 27.4.1914, Амми-Мусса, Алжир), французский историк. Сын крестьянина. В 1936 окончил Сорбонну. В 1932—39 член парижской студенческой коммунистической организации, один из её руководителей. С 1939 член Французской компартии. Во время 2-й мировой войны 1939—45 активный участник Движения Сопротивления. В 1945—60 преподавал в лицеях Парижа, в 1960—1967 в Клермон-Ферранском университете. Ученик Ж. Лефевра , один из крупнейших исследователей истории Великой французской революции, с 1967 занимает кафедру истории Французской революции в Сорбонне и является директором института истории Французской революции (при Сорбонне). Генеральный секретарь «Общества робеспьеристских исследований» (с 1959) и член редколлегии органа этого общества «Annales historiques de la Revolution francaise». С. сосредоточил своё внимание на изучении революции «снизу»; его книга «Парижские санкюлоты...» (1958; сокращённый рус. пер. 1966) — наиболее полное, основанное на архивных материалах исследование о движении парижских народных низов в период якобинской диктатуры. В последующие годы С. опубликовал ряд обобщающих трудов по истории Франции накануне и в период Великой французской революции.

Соч. (кроме указанного в статье): Histoire de la Revolution francaise, v. 1—2, P., 1964; La France a la veille de la Revolution..., 2 ed., P., 1974; Paysans, sansculottes et jacobins, P., 1966; Le Premier empire (1804—1815), P., 1973; в рус. пер. — Из истории Великой буржуазной революции 1789—1794 гг. и революции 1848 г. во Франции, М., 1960; Первая республика. 1792—1804, М., 1974.

Собы'тие,происшествие, важное явление, происшедшее в общественной или личной жизни. О юридическом С. см. Факт юридический , о С. в теории вероятностей см. Случайное событие .

Собэ'к, Собэксан, горный хребет на Ю. Кореи, юго-западная ветвь Восточно-Корейских гор . Длина около 300 км , высота до 1594 м ; является главным водоразделом Южной Кореи. С юга к С. примыкает массив Чирисан (высота до 1915 м ). Сложен главным образом гранитами, гнейсами, кварцитами. Имеет острые гребни и крутые склоны. Месторождения золота (Кимчхон), молибдена (Чансу). На склонах широколиственные (дуб, ясень) и смешанные (с примесью ели, сосны) леса; в южной части — вечнозелёные леса.

Со'ва(Sova) Антонин (26.2.1864, Пацов, — 16.8.1928, там же), чешский поэт. Один из авторов «Манифеста чешской модерны», где выражен протест против современного общества с позиций индивидуального бунта. Трагизм жизни народа и личности в условиях австро-венгерской буржуазной действительности ощутим в сборниках «Реалистические строфы» (1890), «Сочувствие и сопротивление» (1894) и др. В сборниках «Долина нового королевства» (1900), «Лирика любви и жизни» (1907), «Жатва» (1913) выразил абстрактно-романтическую веру в гармонически прекрасное будущее. В творчестве 20-х гг. отразилась противоречивость общественной позиции С. («Кровоточащее братство», 1920; «Весна поэта», 1921; «Дерзкая любовь», 1927). В конце жизни выступал поборником чехословацко-советской дружбы. Мастер пейзажной лирики, С. испытал влияние символизма и импрессионизма. Ввёл в чешскую поэзию свободный стих.

Соч.: Spisy, sv. 1—20. Praha. 1936—38; Basne, Praha, 1933: в рус. пер., в кн.: Антология чешской поэзии, т. 2, М., 1959.

Лит.: Очерки истории чешской литературы XIX—XX вв., М., 1963; Cesti spisovatole z prelomu 19 a 20 stoleti, Praha, 1972.

Сова'та(Sovata), город в Румынии, в уезде Муреш. Климатический и грязевой курорт. Расположен в предгорьях Восточных Карпат. Зима мягкая (средняя температура января —3,4°С), лето тёплое (средняя температура августа 18,7°С); осадков около 700 мм в год. Лечебные средства: рапа и грязь озёр Урсу и Негру; климатотерапия. Лечение больных с заболеваниями женской половой сферы, последствиями травм и заболеваниями периферической нервной системы, костей, мышц, суставов и т.д. Санатории, дома отдыха, грязелечебница, ванное здание; купание в гелиотермах.