БСЭ БСЭ - Большая Советская Энциклопедия (СО)

Лит.: Krzyzanowski L., Gdansk-Sopot-Gdynia, Warsz., 1973.

Сопо'цкин,посёлок городского типа в Гродненском районе Гродненской области БССР, в 27 км к С.-З. от Гродно. Лесозавод. Совхоз по откорму крупного рогатого скота.

Со'почани(Сопоћани, Sopoćani), монастырь на Ю. Сербии, близ г. Нови-Пазар; памятник средневекового сербского искусства. Основан королём Урошем I. Сохранилась церковь св. Троицы (1264—65), однонефная постройка рашской школы, отличающаяся стройностью и композиционной цельностью (открытый притвор и башня западного фасада — конец 13 в.; боковые пристройки в виде пониженных нефов — начало 14 в.). Церковь частично разрушена в конце 14 в. и в 17 в. (реставрирована в 1929, 1948—56). В центральном нефе — первоклассные фрески (около 1265), отличающиеся спокойной величественностью и лиризмом образов, чистым и светлым колоритом, в боковых пристройках фрески конца 13 в., начала 14 в. и 16—17 вв.

Лит.: ћурић В., Сопоћани, Београд, 1963.

Сопра'но(итал. soprano, от sopra — над), 1) самый высокий певческий голос. Диапазон: до 1— до (ре — фа) 3. Необходимое качество С. — хорошо развитый т. н. головной регистр. С. обладают обычно женщины и дети. В хоре особенно красиво звучат голоса мальчиков (т. н. дискантистов). В 16—18 вв. было широко распространено пение кастратов-певцов (называемых также сопранистами). Существует 3 основных разновидности женских С.: драматическое, лирическое и колоратурное. Бывает также лирико-драматическое и лирико-колоратурное С. Драматическое С. отличается силой звучания на всём диапазоне, плотным нижним регистром; лирическому С. свойственны мягкость тембра, гибкость и большая выразительность в кантилене; для колоратурного С. характерны подвижность в исполнении фиоритур, пассажей и т.п., прозрачность тембра, лёгкость и свобода звучания в верхнем регистре. 2) Самая высокая партия в хоре. 3) Высокие по регистру разновидности некоторых музыкальных инструментов.

Соприкаса'ющаяся окру'жностьв точке М кривой l, окружность, имеющая с / в точке М касание порядка n ³ 2 (см. Соприкосновение ). Если кривизна кривой l в точке М равна нулю, то С. о. вырождается в прямую. Т. к. порядок касания / и С. о. в точке М не ниже двух, то С. о. воспроизводит ход кривой вблизи точки касания с точностью до малых 3-го порядка по сравнению с размерами участка кривой. На рисунке изображено обычное (порядок касания кривой и С. о. равен двум) взаимное расположение кривой и её С. о.: кривая пронизывает С. о. в точке соприкосновения. Радиус С. о. называют радиусом кривизны кривой / в точке М, а центр С. о. — центром кривизны. Если кривая l плоская и задана уравнением у = f ( x ) , то радиус С. о. определяется формулой:

.

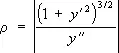Если кривая l — пространственная и задана уравнениями х = х ( u ) , у = у ( u ) , z = z ( u ) , то радиус С. о. определяется формулой:

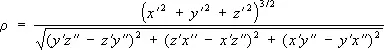
(здесь штрихи означают дифференцирование по параметру u ) .

Иногда С. о. называют соприкасающимся кругом. См. также Дифференциальная геометрия.

Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.

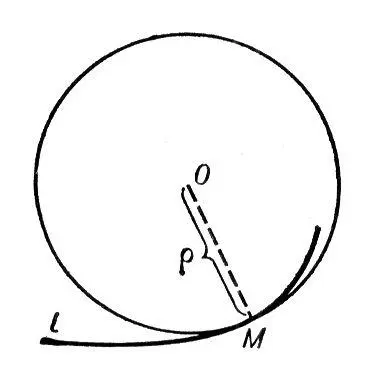
Рис. к. ст. Соприкасающаяся окружность.

Соприкаса'ющаяся пло'скостьв точке М кривой l, плоскость, имеющая с l в точке М касание порядка n ³ 2 (см. Соприкосновение ) . С. п. может быть также определена как предел переменной плоскости, проходящей через три точки кривой /, когда эти точки стремятся к точке М. С механической точки зрения С. п. может быть охарактеризована как плоскость ускорений: при произвольном движении материальной точки по кривой l вектор ускорения лежит в С. п. Обычно кривая, кроме исключит, случаев, пронизывает свою С. п. в точке соприкосновения (см. рис.). Если кривая l задана уравнениями х = х ( u ) , у = у ( u ) , z = z ( u ) , то уравнение С. п. имеет вид:

,

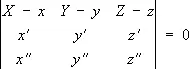где X , Y, Z — текущие координаты, а х, у, z, х', у', z', х’’, у’’, z’’ вычисляются в точке соприкосновения; если все три коэффициента при X, У, Z в уравнении С. п. исчезают, то С. п. делается неопределённой (может совпадать с любой плоскостью, проходящей через касательную). См. также Дифференциальная геометрия.

Лит.: Рашевский П. К., Курс дифференциальной геометрии. 4 изд., М., 1956.

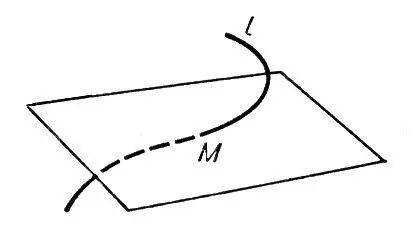
Рис. к ст. Соприкасающаяся плоскость.

Соприкаса'ющаяся сфе'ра вточке М кривой l, сфера, имеющая с / в точке М касание порядка n ³ 3 (см. Соприкосновение ) . С. с. может быть также определена как предел переменной сферы, проходящей через четыре точки кривой /, когда эти точки стремятся к точке М. Если радиус кривизны кривой / в точке М равен r, а s — кручение, то формула для вычисления радиуса С. с. имеет вид:

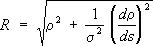
( ds — дифференциал дуги кривой /).

Лит.: Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956.

Соприкаса'ющийся кругв дифференциальной геометрии, см. Соприкасающаяся окружность.

Соприкоснове'ниекривой q с кривой / в данной точке М, геометрическое понятие, означающее, что q имеет с l в точке М касание максимального порядка по сравнению с любой кривой из некоторого заранее данного семейства кривых { q } , включающего q. Порядок касания кривых q и / считается равным п, если отрезок QL есть величина n + 1 порядка малости по отношению к отрезку МК (см. рис., где отрезок QL перпендикулярен к общей касательной кривых q и / в точке М). Таким образом, среди всех кривых семейства { q } С. с кривой / имеет та кривая, которая наиболее тесно прилегает к l (для неё отрезок QL имеет максимальный порядок малости). Кривая семейства { q } , которая имеет С. с кривой l в данной её точке М, называется соприкасающейся кривой данного семейства в указанной точке кривой /. Например, соприкасающейся окружностью в точке М кривой / является окружность, которая в этой точке имеет с / максимальный порядок касания по сравнению с любой другой окружностью.