БСЭ БСЭ - Большая Советская Энциклопедия (СП)

Спили'т-кератофи'ровая форма'ция,комплекс вулканогенных альбитизированных пород — спилитов , кератофиров , их туфов и туфобрекчий, образовавшихся в результате подводных вулканических излияний на ранних стадиях формирования первичных геосинклинальных прогибов. Для С.-к. ф. типично широкое развитие шаровых лав ; в туфах могут встречаться следы морской фауны. Характерное изменение пород С.-к. ф., приводящее к хлоритизации стекла и альбитизации, связывают с метаморфизмом в условиях верхов зеленокаменной фации (см. Фации метаморфизма ).

С.-к. ф. часто является важным компонентом офиолитовых толщ (см. Офиолиты ).

Спили'ты(от греч. spilos — пятно, крапинка), палеотипные базальтовые горные породы, в которых полевой шпат представлен вторичным альбитом; образовались в результате подводных излияний. Структура С. микролитовая, реже диабазовая; образована узкими длинными микролитами альбитизированного плагиоклаза, промежутки между которыми заполнены хлоритом и рудным минералом. С. вместе с кератофирами входят в состав т. н. спилит-кератофировой формации геосинклинальной стадии развития подвижных поясов земной коры.

Спи'лок,слой дермы , полученный при двоении (разделении на слои) полуфабриката в производстве кожи . Различают С. лицевой, средний и мездровый (или бахтармяный). Из тонкого лицевого С. производят фотокожу или галантерейную кожу. Лицевой С. сравнительно большой толщины и средний С. служат для получения кожи, используемой в основном для изготовления обуви. Из бахтармяного С. вырабатывают велюр для обуви и одежды, а также кожи хромового дубления для верха обуви и юфть , имеющие искусственную лицевую поверхность. Мелкий С. и спилковую обрезь (откраиваемые тонкие края) используют для приготовления технического желатина, клея и др. продуктов растворения коллагена .

Спин(от англ. spin — вращаться, вертеться.), собственный момент количества движения элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. (При введении понятия «С.» предполагалось, что электрон можно рассматривать как «вращающийся волчок», а его С. — как характеристику такого вращения, — отсюда название «С.».) С. называется также собственный момент количества движения атомного ядра (и иногда атома); в этом случае С. определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике ) С. элементарных частиц, образующих систему, и орбитальных моментов этих обусловленных их движением системы (см. Ядро атомное ).

С. измеряется в единицах Планка постоянной 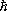и равен 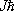, где J — характерное для каждого сорта частиц целое (в т. ч. нулевое) или полуцелое положительное число, называемое спиновым квантовым числом (обычно его называют просто С.). Соответственно говорят, что частица обладает целым или полуцелым С. Например, С. электрона, протона, нейтрона, нейтрино , так же как и их античастиц , в единицах 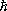равен 1/ 2, С. - и К-мезонов — 0, С. фотона равен 1. Хотя у фотона (как и у нейтрино) нельзя измерить собственный момент количества движения, т. к. нет системы отсчёта, в которой фотон покоится, однако в квантовой электродинамике доказывается, что полный момент фотона в произвольной системе отсчёта не может быть меньше 1; это даёт основание приписать фотону С. 1. Наличие у нейтрино С. 1/ 2вытекает, например, из закона сохранения момента количества движения в процессе бета-распада .

Проекция С. на любое фиксированное направление z в пространстве может принимать значения J , J —1, ..., — J . Т. о., частица со С. J может находиться в 2 J + 1 спиновых состояниях (при J = 1/ 2— в двух состояниях), что эквивалентно наличию у неё дополнительной внутренней степени свободы. Квадрат вектора С., согласно квантовой механике, равен 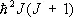. Со С. частицы, обладающей ненулевой массой покоя, связан спиновый магнитный момент 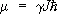, где коэффициент g — магнитомеханическое отношение .

Концепция С. была введена в физику в 1925 Дж. Уленбеком и С. Гаудсмитом , предположившими (на основе анализа спектроскопических данных) существование у электрона собственного механического момента 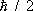и связанного с ним (спинового) магнитного момента, равного магнетону Бора 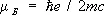(где е и m — заряд и масса электрона, с — скорость света). Т. о., для С. электрона отношение магнитного момента к механическому равно g = е/mс и с точки зрения классической электродинамики является аномальным: для орбитального движения электрона и для любого движения классической системы заряженных частиц с данным отношением е/m оно в 2 раза меньше и равно е /2 mс .

Учёт С. электрона позволил В. Паули сформулировать принцип запрета, утверждающий, что в произвольной физической системе не может быть двух электронов, находящихся в одном и том же квантовом состоянии (см. Паули принцип ). Наличие у электрона С. 1/ 2объяснило мультиплетную структуру атомных спектров ( тонкую структуру ), особенности расщепления спектральных линий в магнитных полях (т. н. аномальный Зеемана эффект ), порядок заполнения электронных оболочек в многоэлектронных атомах (а следовательно, и закономерности периодической системы элементов ), явление ферромагнетизма и многие др. явления.

Существование у протона С. 1/ 2было постулировано на основе опытных данных англ. физиком Д. М. Деннисоном. Эксперимент, проверка этой гипотезы привела к открытию в 1929 орто- и пара-водорода (см. Атом ). Несколько ранее Паули предположил, что сверхтонкая структура атомных уровней энергии определяется взаимодействием электронов со С. ядра, что и было вскоре доказано Г. Бэком и Гаудсмитом в результате анализа эффекта Зеемана в висмуте.

С. частиц однозначно связан с характером статистики, которой подчиняются эти частицы. Как показал Паули (1940), из квантовой теории поля следует, что все частицы с целым С. подчиняются Бозе — Эйнштейна статистике (являются бозонами), с полуцелым С. — Ферми — Дирака статистике (являются фермионами). Для фермионов, например электронов, справедлив принцип Паули, для бозонов он не имеет силы.