БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

В комплексной области С. ф. z aопределяется для всех z ¹ 0 формулой:

, (*)

где k = 0, ± 1, ± 2,.... Если а — целое, то С. ф. z aоднозначна:

.

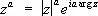Если а — рациональное (а = p/q, где р и q взаимно просты), то С. ф. z a принимает q различных значений:

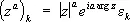
где e k= 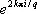— корни степени q из единицы: 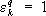и k = 0, 1, …, q - 1. Если а — иррациональное, то С. ф. z a— бесконечнозначна: множитель e a2k p i принимает для разных k различные значения. При комплексных значениях а С. ф. z a определяется той же формулой (*). Например,

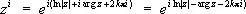
так что, в частности, 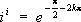, где k = 0, ± 1, ± 2,....

Под главным значением ( z a ) 0 С . ф. понимается её значение при k = 0, если —p< arg z £ p (или 0 £ arg z < 2p). Так, ( z a ) = | z a | e ia arg z, ( i ) 0=e - p/2и т.д.

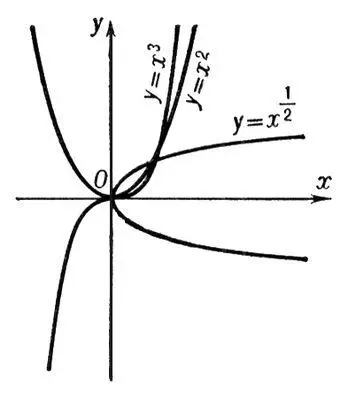
Рис. к ст. Степенная функция.

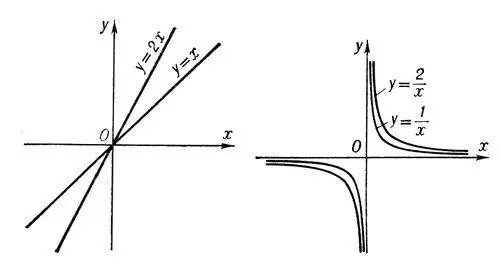
Рис. к ст. Степенная функция.

Степенно'й вы'чет,или вычет степени n по модулю m ( n — целое число, большее единицы, m — целое число). Такое число а, для которого сравнениеx n— а (mod m ) разрешимо. В частности, при n = 2 С. в. называется квадратичным вычетом, при n = 3 — кубическим, при n = 4 — биквадратичным.

Лит.: Виноградов И. М., Основы теории чисел, 8 изд., М., 1972.

Степенно'й ряд, ряд вида a 0+ a 1 z + a 2 z 2+... + a nz n +...,

где коэффициенты a 0, a 1, a 2,..., a n,... — комплексные числа, не зависящие от комплексного переменного z . Областью сходимости С. р. является, вообще говоря, открытый круг D = { z : | z | < R } с центром в точке z = 0. Этот круг называется кругом сходимости С. р., а его радиус R — радиусом сходимости С. р. В частных случаях круг сходимости может вырождаться в точку z = 0 (в этом случае R = 0; пример: 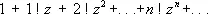) или совпадать со всей комплексной плоскостью ( R = ¥; пример: 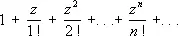). Радиус сходимости С выражается через его коэффициенты по формуле Коши — Адамара

.

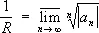Во всех точках круга сходимости С. р. сходится абсолютно; в граничных точках этого круга (в точках окружности | z | = R ) С. р. может как сходиться, так и расходиться. Примеры: 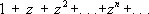, R = 1, ряд расходится в каждой точке окружности ;

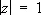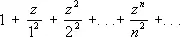, R = 1,

ряд абсолютно сходится во всех точках окружности 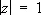. В любой внешней точке круга сходимости (l z l > R ) С. р. расходится. Внутри круга сходимости сумма С. р. 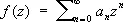является аналитической функцией; производные любого порядка функции f ( z ) можно получить почленным дифференцированием данного ряда, причём С. р. совпадает с Тейлора рядом своей суммы.

А. А. Гончар.

Сте'пень,в первоначальном понимании (целая и положительная С.) есть произведение нескольких равных сомножителей. Обозначение: 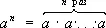, где а — основание, n — показатель степени, a n — степень. С. a 2 называется квадратом, a 3— кубом ( a 2— площадь квадрата, a 3— объём куба со стороной а ) . Основные действия над С. даются формулами: a na m= a n+m; a n: a m= a n-m; (a n) m= a nm . Дальнейшие обобщения С.: нулевая a 0= 1 (при a ¹ 0); отрицательная a -n = 1/ a n ;

дробная 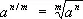(см. Двучленное уравнение, Извлечение корня ) и С. с иррациональным показателем 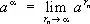, где r п— произвольная последовательность рациональных чисел, стремящаяся к a.

Все указанные выше правила действий справедливы и для обобщённых С. В теории аналитических функций рассматривают также С. с мнимыми основанием и показателем.

Сте'пень диссоциа'ции,отношение числа молекул, распавшихся при диссоциации, к их общему числу.

Сте'пень окисле'ния,то же, что окислительное число.

Сте'пень свобо'ды,одна из характеристик движения механической системы. Подробнее см. в ст. Степеней свободы число.

Сте'пень сжа'тия,отношение объёма рабочего тела в начале сжатия к объёму его в конце сжатия в цилиндре двигателя внутреннего сгорания. С увеличением С. с. рабочее тело (горючая смесь в карбюраторных двигателях, воздух в дизелях) в конце хода сжатия занимает меньший объём, давление и температура его повышаются и процесс сгорания протекает быстрее и с меньшими потерями тепла. Повышение С. с. увеличивает мощность и улучшает топливную экономичность двигателя, однако оно ограничивается стойкостью топлива по отношению к детонации. С. с . карбюраторных двигателей 6,5—9,5, дизелей 16—21.

Сте'пи,тип растительности, представленный сообществами из засухо- и морозоустоичивых многолетних травянистых растений с господством дерновинных злаков, реже осок и луков. С. связаны преимущественно с чернозёмами и каштановыми почвами и засушливым климатом, с максимумом осадков в летние месяцы. Занимают наибольшие площади во внутриконтинентальных частях Северного полушария в пределах умеренного пояса, где зоны степей вытянуты с З. на В. в Европе и Азии и с С. на Ю. в Северной Америке. С. имеются также в Южной Америке. На значительной территории распаханы (например, в Европе сохранились главным образом в заповедниках).