БСЭ БСЭ - Большая Советская Энциклопедия (СТ)

Стью'дента крите'рий,статистическое правило проверки гипотез (см. Статистическая проверка гипотез ) , основанное на Стьюдента распределении.

Стью'дента распределе'ниес f степенями свободы, распределение отношения Т = X/Y независимых случайных величин Х и Y, где Х подчиняется нормальному распределению с математическим ожиданием EX = 0 и дисперсией DX = 1, а fY 2имеет «Хи-квадрат» распределение с f степенями свободы. Функция распределения Стьюдента выражается интегралом

.

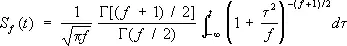Если X 1,..., X n— независимые случайные величины, одинаково нормально распределённые, причём EX i = a и DX i= s 2 ( i = 1,..., n ) , то при любых действительных значениях а и s > 0 отношение 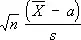подчиняется С. р. с f = п- 1 степенями свободы (здесь 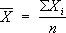и 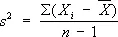). Это свойство было впервые (1908) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = a 0( a 0= заданное число, дисперсия s 2предполагается неизвестной). Гипотезу а = a 0считают не противоречащей результатам наблюдений X 1,..., X n, если справедливо неравенство 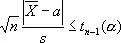, в противном случае гипотеза а = а 0отвергается (так называемый критерий Стьюдента). Критическое значение t = t n-1( a ) представляет собой решение уравнения S n-1( t ) = 1 – 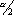, a — заданный значимости уровень (0 < a < ). Если проверяемая гипотеза а = а 0верна, то критерий Стьюдента, соответствующий критическому значению t n–1( a ) , может её ошибочно отвергнуть с вероятностью а .

С. р. используется для решения множества др. задач математической статистики (см. Малые выборки, Ошибок теория, Наименьших квадратов метод ) .

Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.

Стэ'нли водопа'ды(Stanley Falls), водопады в верхнем течении р. Конго (Заир), между гг. Убунду и Кисангани, на территории Республики Заир. 7 значительных порогов, разделённых плёсами, на расстоянии около 150 км; общее падение около 40 м. Назван в честь Г. М. Стэнли.

Стэ'нли(Stanley) Генри Мортон [настоящие имя и фамилия — Джон Роулендс (Rowlands)] (28.1.1841, Денби, Уэльс,— 10.5.1904, Лондон), журналист, исследователь Африки. В возрасте 17 лет эмигрировал из Великобритании в США. В 1871—72 в качестве корреспондента газеты «Нью-Йорк геральд» проник с В. в глубь Африки в поисках пропавшего без вести Д. Ливингстона. Встретил его у озера Танганьика и обследовал вместе с ним это озеро. В 1874—77 пересек Африку с В. на З. во главе англо-американской экспедиции. Из Занзибара С. дошёл до озера Виктория и установил его очертания. Открыл горный массив Рувензори и озёра Эдуард (Иди-Амин-Дада) и Джордж; исследовал течение р. Кагера, объехал озеро Танганьика, затем достиг р. Луалаба и выяснил, что она является верховьем р. Конго (Заир); по этой реке спустился вниз до устья, положив на карту неизвестную европейцам среднюю часть её течения. В 1879—84, находясь на службе у бельгийского короля Леопольда II, участвовал в захвате бассейна р. Конго; попутно разведал ряд её притоков и открыл озёра Леопольда II (Маи-Ндомбе) и Тумба. В 1887—89 во главе английской экспедиции вновь пересек Африку (с З. на В.); исследовал р. Арувими, установил, что озеро Эдуард принадлежит к системе Нила. Именем С. названы водопады в верховье Конго.

Соч.: Through the dark continent..., v. 1—2, L., 1878; In darkest Africa...,v. 1—2, L., 1890; в рус. пер.: Как я отыскал Ливингстона, СПБ, 1874; В дебрях Африки, 3 изд., М., 1958.

Лит.: Горнунг М.Б.,Липец Ю.Г., Олейников И. Н., История открытия и исследования Африки, М., 1973.

И. Н. Олейников.

Г. М. Стэнли.

Стэ'нли(Stanley), главный город Фолклендских островов; см. Порт-Стэнли.

Стэ'нли(Stanley) Уэнделл Мередит (р. 16.8.1904, Риджвилл, штат Индиана), американский вирусолог и биохимик. Член Национальной АН США (1941) и Нью-Йоркской АН (1963). В 1926 окончил Эрлемский колледж в Ричмонде (штат Индиана). С 1929 работал в Иллинойсском университете, с 1930 в Мюнхенском университете. В 1931 вернулся в США, в Рокфеллеровский институт медицинских исследований (Нью-Йорк), с 1932 в Рокфеллеровском институте в Принстоне. С 1948 профессор Калифорнийского университета в Беркли. Основные работы посвящены химическому составу вирусов, их биохимии, репродукции, мутациям, проблеме рака. В 1935 впервые очистил и выделил в кристаллическом виде вирус мозаики табака, открыв путь для получения чистых препаратов вирусов и их изучения. В 1955 выделил вирус полиомиелита. Нобелевская премия по химии (1946, совместно с Дж. Самнером и Дж. Нортропом).

Соч. в рус. пер.: Вирусы и природа жизни, М., 1963 (совм. с Э. Взленсом).

У. М. Стэнли.

Стэнливи'ль(Stanleyville), до 1966 название г. Кисангани в Республике Заир.

Стэ'нли-Пул(Stanley Pool), озеровидное расширение в среднем течении р. Конго (Заир), непосредственно выше входа реки в долину прорыва через береговую Южно-Гвинейскую возвышенность. Длина около 30 км, ширина до 25 км. Площадь 555 км 2 . Глубина до 25 м. Остров Баму разделяет С.-П. на 2 рукава с мелкими островками и песчаными отмелями, затопляемыми в период высокой воды. У юго-западной оконечности С.-П. расположены столицы государств Заира (Киншаса, на левом берегу) и Конго (Браззавиль, на правом берегу) — важные речные порты.

Стэ'нтона число',один из подобия критериев тепловых процессов, характеризующий интенсивность диссипации энергии в потоке жидкости или газа: St = a / c p rv, где a — коэффициент теплоотдачи, с r — удельная теплоёмкость среды при постоянном давлении, r — плотность, v — скорость течения. Названо по имени английского учёного Т. Стэнтона (Th. Stanton; 1865—1931). С. ч. является безразмерной формой коэффициента теплоотдачи и связано с Нуссельта числомNu и Пекле числомРе соотношением: St = Nu / Pe. С. ч. выражается также через безразмерные коэффициенты поверхностного трения C fили гидродинамического сопротивления l . В случае Pr = 1 (см. Прандтля число ), St = C f/2 = l/8.