БСЭ БСЭ - Большая Советская Энциклопедия (СЖ)

Сжа'тиев сопротивлении материале в, см. Растяжение-сжатие .

Сжа'тие земли',земного эллипсоида, величина, характеризующая степень сплюснутости Земли в направлении оси вращения, т. е. отступление формы Земли от шара. Полярное С. З. a выражается равенством: 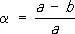, где a — радиус экватора Земли, а b — полярный радиус её. По современным данным, a = 1: 298,3. В связи с обнаруженным фактом сплюснутости Земли также и по экватору введено понятие экваториального С. З., равного 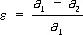, где a 1 и a 2 , соответственно, — наибольший и наименьший радиусы земного экватора. По имеющимся данным, e = 1: 30000, разность a 1— a 2 составляет около 210 м . См. также Геодезия , Земля .

Сжа'тых отображе'ний при'нцип,одно из основных положений теории метрических пространств о существовании и единственности неподвижной точки множества при некотором специальном («сжимающем») отображении его в себя. С. о. п. применяют главным образом в теории дифференциальных и интегральных уравнений.

Произвольное отображение А метрического пространства М в себя, которое каждой точке х из М сопоставляет некоторую точку у = Ax из М , порождает в пространстве М уравнение

Ax = х . (*)

Действие отображения А на точку х можно интерпретировать как перемещение её в точку у = Ax . Точка х называется неподвижной точкой отображения А , если выполняется равенство (*). Т. о. вопрос о разрешимости уравнения (*) является вопросом о нахождении неподвижных точек отображения А .

Отображение А метрического пространства М в себя называется сжатым, если существует такое положительное число a < 1, что для любых точек х и у из М выполняется неравенство

d ( Ax, Ау ) £ a d ( х, у ),

где символ d ( u, u) означает расстояние между точками u и u метрического пространства М .

С. о. п. утверждает, что каждое сжатое отображение полного метрического пространства в себя имеет, и притом только одну, неподвижную точку. Кроме того, для любой начальной точки x 0 из М последовательность { x n }, определяемая рекуррентными соотношениями

x n= Ax n-1 , n = 1,2,...,

имеет своим пределом неподвижную точку х отображения А . При этом справедлива следующая оценка погрешности:

.

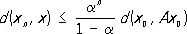С. о. п. позволяет единым методом доказывать важные теоремы о существовании и единственности решений дифференциальных, интегральных и др. уравнений. В условиях применимости С. о. п. решение может быть с наперёд заданной точностью вычислено последовательных приближений методом .

С помощью определённого выбора полного метрического пространства М и построения отображения А эти задачи сводят предварительно к уравнению (*), а затем находят условия, при которых отображение А оказывается сжатым.

Лит.: Смирнов В. И., Курс высшей математики, т. 5, М., 1959.

Ш. А. Алимов.

Сжиже'ние га'зов,переход вещества из газообразного состояния в жидкое. С. г. достигается охлаждением их ниже критической температуры ( Т к ) и последующей конденсацией в результате отвода теплоты парообразования (конденсации). Охлаждение газа ниже Т К необходимо для достижения области температур, при которых газ может сконденсироваться в жидкость (при Т > Т К жидкость существовать не может). Впервые газ (аммиак) был сжижен в 1792 (голландский физик М. ван Марум). Хлор был получен в жидком состоянии в 1823 (М. Фарадей ), кислород — в 1877 (швейцарский учёный Р. Пикте и французский учёный Л. П. Кальете), азот и окись углерода — в 1883 (З. Ф. Вроблевский и К. Ольшевский ), водород — в 1898 (Дж. Дьюар ), гелий — в 1908 (Х. Камерлинг-Оннес ).

Идеальный процесс С. г. изображен на рис. 1 . Изобара 1—2 соответствует охлаждению газа до начала конденсации, изотерма 2—0 — конденсации газа. Площадь ниже 1—2—0 эквивалентна количеству теплоты, которое необходимо отвести от газа при его сжижении, а площадь внутри контура 1—2—0—3 ( 1—3 — изотермическое сжатие газа, 3—0 — адиабатическое его расширение) характеризует термодинамически минимальную работу L min , необходимую для С. г.:

L min = T 0 ( S Г— S Ж ) — ( J Г- J Ж ),

где T 0 — температура окружающей среды; S Г , S Ж — энтропии газа и жидкости; J Г , J Ж — теплосодержания (энтальпии) газа и жидкости.

Значения L min и действительно затрачиваемой работы L Д для сжижения ряда газов даны в таблице.

Промышленное С. г. с критической температурой Т К выше температуры окружающей среды (например, аммиак, хлор) осуществляется с помощью компрессора, где газ сжимается, и последующей конденсацией газа в теплообменниках, охлаждаемых водой или холодильным рассолом. С. г. с Т К , которая значительно ниже температуры окружающей среды, производится методами глубокого охлаждения . Наиболее часто для С. г. с низким Т К применяются холодильные циклы , основанные на дросселировании сжатого газа (использование Джоуля — Томсона эффекта ), на расширении сжатого газа с производством внешней работы в детандере, на расширении газа из постоянного объёма без совершения внешней работы (метод теплового насоса ). В лабораторной практике иногда используется каскадный метод охлаждения (сжижения).

Графическое изображение и схема дроссельного цикла С. г. дана на рис. 2 . После сжатия в компрессоре ( 1—2 ) газ последовательно охлаждается в теплообменниках ( 2—3—4 ) и затем расширяется (дросселируется) в вентиле ( 4—5 ). При этом часть газа сжижается и скапливается в сборнике, а несжижившийся газ направляется в теплообменники и охлаждает свежие порции сжатого газа. Для С. г. по циклу с дросселированием необходимо, чтобы температура сжатого газа перед входом в основной теплообменник T3 была ниже температуры инверсионной точки (см. Инверсионная кривая ). Для этого и служит теплообменник с посторонним холодильным агентом T2. Если температура инверсионной точки газа лежит выше комнатной (азот, аргон, кислород), то схема принципиально работоспособна и без теплообменников T1 и T2. Применение посторонних хладагентов в этих случаях имеет целью повышение выхода жидкости. Если же температура инверсионной точки газа ниже комнатной, то теплообменник с посторонним хладагентом обязателен. Например, при сжижении водорода методом дросселирования в качестве постороннего хладагента используется жидкий азот, при сжижении гелия — жидкий водород.