БСЭ БСЭ - Большая Советская Энциклопедия (ТО)

Важные классы топологических пространств получаются наложением так называемых аксиом отделимости. Примером является так называемая аксиома Хаусдорфа, или аксиома T 2, требующая, чтобы любые две различные точки обладали непересекающимися окрестностями. Топологическое пространство, удовлетворяющее этой аксиоме, называется хаусдорфовым, или отделимым. Некоторое время в математической практике встречались почти исключительно хаусдорфовы пространства (например, любое метрическое пространство хаусдорфово). Однако роль нехаусдорфовых топологических пространств в анализе и геометрии постоянно растет.

Топологические пространства, являющиеся подпространствами хаусдорфовых (би) компактных пространств, называются вполне регулярными или тихоновскими. Их тоже можно охарактеризовать некоторой аксиомой отделимости, а именно: аксиомой, требующей, чтобы для любой точки x 0 Х и любого не содержащего её замкнутого множества F Х существовала непрерывная функция g : Х ® [0, 1], равная нулю в x 0 и единице на F .

Топологические пространства, являющиеся открытыми подпространствами хаусдорфовых компактных, называются локально компактными пространствами. Они характеризуются (в классе хаусдорфовых пространств) тем, что каждая их точка обладает окрестностью с компактным замыканием (пример: евклидово пространство). Любое такое пространство дополняется одной точкой до компактного (пример: присоединением одной точки из плоскости получается сфера комплексного переменного, а из — сфера S n ).

Отображение f : X ® Y топологическое пространства Х в топологическое пространство Y называют непрерывным отображением, если для любого открытого множества V Ì Y множество f —1 ( V ) открыто в X . Непрерывное отображение называют гомеоморфизмом, если оно взаимно однозначно и обратное отображение f —1: Y ® X непрерывно. Такое отображение устанавливает взаимно однозначное соответствие между открытыми множествами топологических пространств Х и Y , перестановочное с операциями объединения и пересечения множеств. Поэтому все топологические свойства (то есть свойства, формулируемые в терминах открытых множеств) этих пространств одни и те же, и с топологической точки зрения гомеоморфные топологические пространства (то есть пространства, для которых существует хотя бы один гомеоморфизм Х ® Y ) следует считать одинаковыми (подобно тому как в евклидовой геометрии одинаковыми считаются фигуры, которые можно совместить движением). Например, гомеоморфны («топологически одинаковы») окружность и граница квадрата, шестиугольника и т.п. Вообще любые две простые (не имеющие двойных точек) замкнутые линии гомеоморфны. Напротив, окружность не гомеоморфна прямой (ибо удаление точки не нарушает связности окружности, но нарушает связность прямой; по той же причине прямая не гомеоморфна плоскости, а окружность не гомеоморфна «восьмёрке»). Окружность не гомеоморфна также и плоскости (выкиньте не одну, а две точки).

Пусть { Х a} — произвольное семейство топологических пространств. Рассмотрим множество Х всех семейств вида { х a} , где x a X a(прямое произведение множеств X a). Для любого a формула 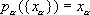определяет некоторое отображение 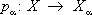(называется проекцией). Вообще говоря, в Х можно ввести много топологических структур, относительно которых все отображения p aнепрерывны. Среди этих структур существует наименьшая (то есть содержащаяся в любой такой структуре). Снабженное этой топологической структурой множество Х называется топологическим произведением топологических пространств Х aи обозначается символом ПХ a(а в случае конечного числа сомножителей — символом X 1 ´ ... ´ X n ). В явном виде открытые множества пространства Х можно описать как объединения конечных пересечений всех множеств вида 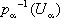, где U aоткрыто в X a. Топологическое пространство Х обладает следующим замечательным свойством универсальности, однозначно (с точностью до гомеоморфизма) его характеризующим: для любого семейства непрерывных отображений f a: Y ® X aсуществует единственное непрерывное отображение f : Y ® X , для которого 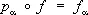при всех a. Пространство 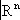является топологическим произведением n экземпляров числовой прямой. Одной из важнейших теорем общей Т. является утверждение о том, что топологическое произведение компактных топологических пространств компактно.

Если Х — топологическое пространство, а Y — произвольное множество и если задано отображение p : X ® Y пространства Х на множество Y (например, если Y является фактормножеством Х по некоторому отношению эквивалентности, а p представляет собой естественную проекцию, сопоставляющую с каждым элементом х Î Х его класс эквивалентности), то можно ставить вопрос о введении в Y топологической структуры, относительно которой отображение p непрерывно. Наиболее «богатую» (открытыми множествами) такую структуру получают, полагая открытыми множествами в Y все те множества V Ì Y, для которых множество f ‑1 ( V ) Ì Х открыто в X . Снабженное этой топологической структурой множество Y называется факторпространством топологического пространства Х (по отношению к p ). Оно обладает тем свойством, что произвольное отображение f : Y ® Z тогда и только тогда непрерывно, когда непрерывно отображение 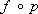: X ® Z. Непрерывное отображение p : X ® Y называется факторным, если топологическое пространство Y является по отношению к p факторпространством топологического пространства X . Непрерывное отображение p : X ® Y называется открытым, если для любого открытого множества U Ì Х множество p(U) открыто в Y , и замкнутым, если для любого замкнутого множества F Ì Х множество p(F) замкнуто в Y . Как открытые, так и замкнутые непрерывные отображения f : Х ® Y , для которых f(X) = Y , являются факторными.