БСЭ БСЭ - Большая Советская Энциклопедия (ТР)
- Название:Большая Советская Энциклопедия (ТР)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ТР) краткое содержание
Большая Советская Энциклопедия (ТР) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
С помощью основных Т. ф. можно определить другие Т. ф.: тангенс tgj = sinj /cosj, котангенс ctgj = cosj /sinj, секанс secj = 1/cosj, косеканс cosecj = 1/sinj. При этом tgj и secj определяются только для таких j, для которых cosj ¹ 0; а ctgj и cosecj для тех j, для которых sinj ¹ 0; функция secj — чётная, а функции cosecj, tgj и ctgj — нечётные. Эти функции также могут быть представлены геометрически отрезками прямых ( рис. 1 ): tgj = AL , ctgj = BK , secj = OL , cosecj = OK (для острых углов j и соответствующими отрезками для других углов). С этим геометрическим представлением связано и происхождение названий Т. ф. Так, латинское tangens означает касательную (tgj изображается отрезком AL касательной к окружности), secans — секущую (secj изображается отрезком OL секущей к окружности). Название «синус» (лат. sinus — изгиб, пазуха) представляет собой перевод арабского «джайб», являющегося, по-видимому, искажением санскритского слова «джива» (буквально — тетива лука), которым индийские математики обозначали синус. Названия «косинус», «котангенс», «косеканс» представляют собой сокращения термина complementi sinus (синус дополнения) и ему подобных, выражающих тот факт, что cosj, ctgj и cosecj равны соответственно синусу, тангенсу и секансу аргумента (дуги или угла), дополнительного к j (до или, в градусной мере, до 90°):
cosj = sin ( — j); ctgj = tg ( — j);
cosecj = sec ( — j).
Подобно синусу и косинусу, остальные Т. ф. для острых углов могут рассматриваться как отношения сторон прямоугольного треугольника: тангенс и котангенс как отношения катетов (противолежащего к прилежащему и наоборот), а секанс и косеканс как отношения гипотенузы соответственно к прилежащему и противолежащему катетам.
Так как точка С, являющаяся концом дуги j, служит одновременно концом дуг j + 2p, j + 4p, ¼ (2p — длина окружности), то все Т. ф. оказываются периодическими. При этом основным периодом функций sinj, cosj, secj, cosecj является число 2p (угол в 360°), а основным периодом tgj и ctgj — число p (угол в 180°). Графики Т. ф. см. на рис. 2.
Значения Т. ф. одного и того же аргумента связаны между собой рядом соотношений:
sin 2j + cos 2j = 1,
tg 2j + 1 = sec 2j; ctg 2j + 1 = cosec 2j.
Для некоторых значений аргумента значения Т. ф. могут быть получены из геометрических соображений (табл.).
| Аргумент | Тригонометрические функции | ||||||
| в градусах | в радианах | sinj | cosj | tgj | ctgj | secj | cosecj |
| 0˚ | 0 | 0 | 1 | 0 | не существует | 1 | не существует |
| 30˚ | p/6 | 1/ 2 | Ö3/2 » 0,8660 | Ö3/3 » 0,5774 | Ö3 » 1,7322 | 2Ö3/3 » 1,1547 | 2 |
| 45˚ | p/4 | Ö2/2 » 0,7071 | Ö2/2 » 0,7071 | 1 | 1 | Ö2 » 1,4142 | Ö2 » 1,4142 |
| 60˚ | p/3 | Ö3/2 » 0,8660 | 1/ 2 | Ö3 » 1,7322 | Ö3/3 » 0,5774 | 2 | 2Ö3/3 » 1,1547 |
| 90˚ | p/2 | 1 | 0 | не существует | 0 | не существует | 1 |
Для больших значений аргумента можно пользоваться так называемыми формулами приведения, которые позволяют выразить Т. ф. любого аргумента через
Т. ф. аргумента j, удовлетворяющего соотношению 0 £ j £ или даже 0 £ j £ , что упрощает составление таблиц Т. ф. и пользование ими, а также построение графиков. Эти формулы имеют вид:
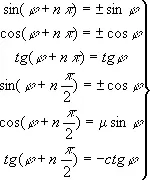 (1)
(1)
в первых трёх формулах n может быть любым целым числом, причём верхний знак соответствует значению n = 2 k , а нижний — значению n = 2 k + 1; в последних — n может быть только нечётным числом, причём верхний знак берётся при n = 4 k + 1, а нижний при n = 4 k — 1.
Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т. ф. суммы или разности значений аргумента через Т. ф. этих значений:
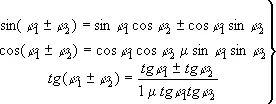 (2)
(2)
знаки в левой и правой частях всех формул согласованы, то есть верхнему (нижнему) знаку слева соответствует верхний (нижний) знак справа. Из них, в частности, получаются формулы для Т. ф. кратных аргументов, например:
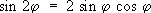
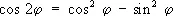
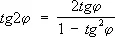
Часто бывают полезны формулы, выражающие степени sin и cos простого аргумента через sin и cos кратного, например:
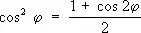 ,
, 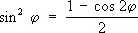 .
.
Формулы для cos 2j и sin 2j можно использовать для нахождения значений Т. ф. половинного аргумента:
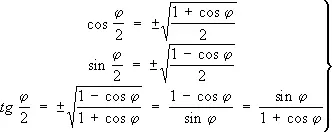 (3)
(3)
Знак перед корнем выбирается в зависимости от величины .
Суммы или разности Т. ф. различных аргументов могут быть преобразованы в произведения по следующим формулам:
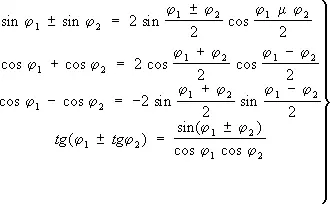 (4)
(4)
в первой и последней формулах (4) знаки согласованы. Наоборот, произведения Т. ф. могут быть преобразованы в сумму или разность по формулам:
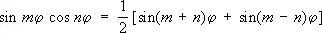 ;
;
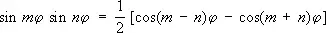 ;
;
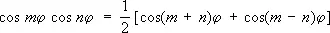 .
.
Производные всех Т. ф. выражаются через Т. ф.:
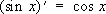 ;
;
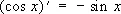 ;
;
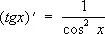 ;
;
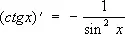 ;
;
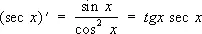 ;
;
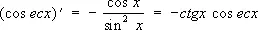 .
.
При интегрировании Т. ф. получаются Т. ф. или их логарифмы:
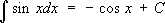 ,
,
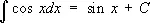 ,
,
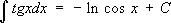 ,
,
Интервал:
Закладка:
