БСЭ БСЭ - Большая Советская Энциклопедия (ТЕ)

Лит.: Гребер Г., Эрк С., Григулль У., Основы учения о теплообмене, пер. с нем., М., 1958; Шорин С. Н., Теплопередача, 2 изд., М., 1964; Михеев М. А., Михеева И. М., Основы теплопередачи, 2 изд., М., 1973.

И. Н. Розенгауз.

Теплопрово'дности уравне'ние, дифференциальное уравнение с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности. Т. у. выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды Т. у. имеет вид:

,

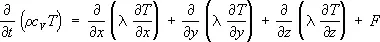где r — плотность среды; c v— теплоёмкость среды при постоянном объёме; t — время; х, у, z — координаты; Т = Т ( х, у, z, t ) — температура, которая вычисляется при помощи Т. у.; l — коэффициент теплопроводности; F = F ( x, y, z, t ) — заданная плотность тепловых источников. Величины r, C v, l зависят от координат и, вообще говоря, от температуры. Для анизотропной среды Т. у. вместо l содержит тензор теплопроводности l ir , где i, k = 1, 2, 3.

В случае изотропной однородной среды Т. у. принимает вид:

,

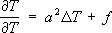где D T — Лапласа оператор, a 2= l /(r c v) — коэффициент температуропроводности; f = F/ ( rc v ) . В стационарном состоянии, когда температура не меняется со временем, Т. у. переходит в Пуассона уравнение D Т = f / a 2= F /l или, при отсутствии источников теплоты, в Лапласа уравнение D Т = 0. Основными задачами для Т. у. является Коши задача и смешанная краевая задача (см. Краевые задачи ) .

Первые исследования Т. у. принадлежат Ж. Фурье (1822) и С. Пуассону (1835). Важные результаты в исследовании Т. у. были получены И. Г. Петровским, А. Н. Тихоновым, С. Л. Соболевым.

Лит.: Карслоу Г. С., Теория теплопроводности, пер. с англ., М.— Л., 1947: Владимиров В. С., Уравнения математической физики, М., 1967; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

Д. Н. Зубарев.

Теплопрово'дность,один из видов переноса теплоты (энергии теплового движения микрочастиц) от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры. При Т. перенос энергии в теле осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией. Если относительное изменение температуры Т на расстоянии средней длины свободного пробега частиц l мало, то выполняется основной закон Т. (закон Фурье): плотность теплового потока q пропорциональна градиенту температуры grad T, то есть

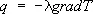, (1)

где l — коэффициент Т., или просто Т., не зависит от grad T [l зависит от агрегатного состояния вещества (см. табл. ), его атомно-молекулярного строения, температуры и давления, состава (в случае смеси или раствора) и т. д.].

Значения коэффициента теплопроводности l для некоторых газов, жидкостей и твёрдых тел при атмосферном давлении

Отклонения от закона Фурье могут появиться при очень больших значениях grad T (например, в сильных ударных волнах ) , при низких температурах (для жидкого гелия Не II) и при высоких температурах порядка десятков и сотен тысяч градусов, когда в газах перенос энергии осуществляется не только в результате межатомных столкновений, но в основном за счёт излучения (лучистая Т.). В разреженных газах, когда l сравнимо с расстоянием L между стенками, ограничивающими объём газа, молекулы чаще сталкиваются со стенками, чем между собой. При этом нарушается условие применимости закона Фурье и само понятие локальной температуры газа теряет смысл. В этом случае рассматривают не процесс Т. в газе, а теплообмен между телами, находящимися в газовой среде. Процесс переноса теплоты —Т. — в сплошной среде описывается теплопроводности уравнением.

Для идеального газа, состоящего из твёрдых сферических молекул диаметром d, согласно кинетической теории газов, справедливо следующее выражение для \ (при ):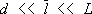

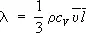, (2)

где r — плотность газа, c v — теплоёмкость единицы массы газа при постоянном объёме V, 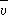— средняя скорость движения молекул. Поскольку J пропорциональна 1 /р, а r ~ р ( р — давление газа), то Т. такого газа не зависит от давления. Кроме того, коэффициент Т. l и вязкости m связаны соотношением: 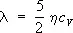. В случае газа, состоящего из многоатомных молекул, существенный вклад в l дают внутренние степени свободы молекул, что учитывает соотношение:

,

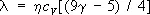где g = ср/c v , ср — теплоёмкость при постоянном давлении. В реальных газах коэффициент Т. — довольно сложная функция температуры и давления, причём с ростом Т и р значение l возрастает. Для газовых смесей l может быть как больше, так и меньше коэффициента Т. компонентов смеси, то есть Т. — нелинейная функция состава.

В плотных газах и жидкостях среднее расстояние между молекулами сравнимо с размерами самих молекул, а кинетическая энергия движения молекул того же порядка, что и потенциальная энергия межмолекулярного взаимодействия. В связи с этим перенос энергии столкновениями происходит значительно интенсивнее, чем в разреженных газах, и скорость передачи энергии молекул от горячих изотермических слоев жидкости к более холодным близка к скорости распространения малых возмущений давления, равной скорости звука, т. е. 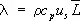, где u s — скорость звука в жидкости, 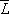— среднее расстояние между молекулами. Эта формула лучше всего выполняется для одноатомных жидкостей. Как правило, l жидкостей убывает с ростом Т и слабо возрастает с ростом р. Т. твёрдых тел имеет различную природу в зависимости от типа твёрдого тела. В диэлектриках, не имеющих свободных электрических зарядов, перенос энергии теплового движения осуществляется фононами — квазичастицами, квантами упругих колебаний атомов кристалла (см. Колебания кристаллической решётки, Квазичастицы ) . У твёрдых диэлектриков 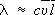, где с — теплоёмкость диэлектрика, совпадающая с теплоёмкостью газа фононов, 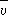— средняя скорость движения фононов, приблизительно равная скорости звука, 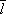— средняя длина свободного пробега фононов. Существование определённого конечного значения l — следствие рассеяния фононов на фононах, на дефектах кристаллической решётки (в частности, на границах кристаллитов и на границе образца). Температурная зависимость л. определяется зависимостью от температуры с и l . При высоких температурах ( T >> Q D , где Q D— Дебая температура ) главным механизмом, ограничивающим l , служит фонон-фононное рассеяние, связанное с ангармонизмом колебаний атомов кристалла. фонон-фононный механизм теплосопротивления (1/l — коэффициент теплосопротивления) возможен только благодаря процессам переброса (см. Твёрдое тело ) , в результате которых происходит торможение потока фононов. Чем Т выше, тем с большей вероятностью осуществляются процессы переброса, а l уменьшается: при T >> Q D l ~ 1 /T и, следовательно, l ~ 1/ T , так как с в этих условиях слабо зависит от Т . С уменьшением Т (при T << Q D ) длина свободного пробега, определяемая фонон-фононным рассеянием, резко растет ( 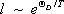) и, как правило, ограничивается размерами образца ( R ) . Теплоёмкость при T << Q Dубывает ~ Т 3благодаря чему l при понижении температуры проходит через максимум. Температура, при которой l имеет максимум, определяется из равенства l ( T ) » R.