БСЭ БСЭ - Большая Советская Энциклопедия (УП)

При испытаниях образцов, вырезанных из изотропного материала по разным направлениям, получаются одни и те же значения Е, G и n. В среднем изотропны многие конструкционные металлы и сплавы, резина, пластмассы, стекло, керамика, бетон. Для анизотропного материала (древесина, кристаллы, армированные бетон и пластики, слоистые горные породы и др.) упругие свойства зависят от направления. Напряжение в любой точке тела характеризуется шестью величинами – компонентами напряжений: нормальными напряжениями s хх , s уу , s zz и касательными напряжениями s ху , s уz , s zx , Причём s ху = s ухи т.д. Деформация в любой точке тела также характеризуется шестью величинами – компонентами деформаций: относительными удлинениями e хх , e уу , e zzи сдвигами e ху , e уz , e zx , Причём e ху= e ухи т.д.

Основным физическим законом У. т. является обобщённый Гука закон, согласно которому нормальные напряжения линейно зависят от деформаций. Для изотропных материалов эти зависимости имеют вид:

, , ,

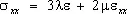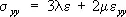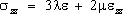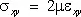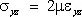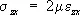, , , (1)

где 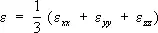- средняя (гидростатическая) деформация, l и m = G – Ламе постоянные. Т. о., упругие свойства изотропного материала характеризуются двумя постоянными l и m или какими-нибудь выраженными через них двумя модулями упругости.

Равенство (1) можно также представить в виде

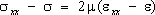, ..., (2)

, …,

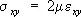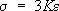
где 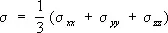– среднее (гидростатическое) напряжение, К – модуль всестороннего сжатия.

Для анизотропного материала 6 зависимостей между компонентами напряжений и деформаций имеют вид:

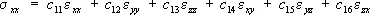(3)

...............................................................

Из входящих сюда 36 коэффициентов c ij называются модулями упругости, 21 между собой независимы и характеризуют упругие свойства анизотропного материала.

Для нелинейного упругого изотропного материала в равенствах (2) всюду вместо m входит коэффициент 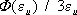, а соотношение 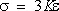заменяется равенством 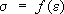, где величина e uназывается интенсивностью деформации, а функции Ф и f , универсальные для данного материала, определяются из опытов. Когда Ф (e u) достигает некоторого критического значения, возникают пластические деформации. Законы пластичности при пропорциональном возрастании нагрузок или напряжений (простое нагружение) имеют тот же вид, но с др. значениями функций Ф и f (законы теории малых упруго-пластических деформаций), а при уменьшении напряжений (разгрузке) имеют место соотношения (1) или (2), в которых вместо s ijи e ij подставляются их приращения (разности двух текущих значений).

Математическая задача У. т. при равновесии состоит в том, чтобы, зная действующие внешние силы (нагрузки) и т. н. граничные условия, определить значения в любой точке тела компоненты напряжений и деформаций, а также компоненты u x , u y , и z ; вектора перемещения каждой частицы тела, т. е. определить эти 15 величин в виде функций от координат x , у, z точек тела. Исходными для решения этой задачи являются дифференциальные уравнения равновесия:

,

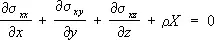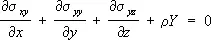, (4)

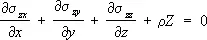
где r – плотность материала, XYZ – проекции на координатные оси действующей на каждую частицу тела массовой силы (например, силы тяжести), отнесённые к массе этой частицы.

К трём уравнениям равновесия присоединяются 6 равенств (1) в случае изотропного тела и ещё 6 равенств вида:

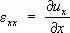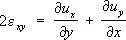, …, , …, (5)

устанавливающих зависимости между компонентами деформаций и перемещений.

Когда на часть S 1граничной поверхности тела действуют заданные поверхностные силы (например, силы контактного взаимодействия), проекции которых, отнесённые к единице площади, равны F x , F y , F z , а для части S 2этой поверхности заданы перемещения её точек j х , j у , j z, граничные условия имеют вид:

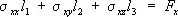(на S 1) (6)

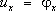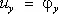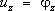, , (на S 2) (7)

где l 1 , l 2 , l 3 – косинусы углов между нормалью к поверхности и координатными осями. Первые условия означают, что искомые напряжения должны удовлетворять на границе S 1трём равенствам (6), а вторые – что искомые перемещения должны удовлетворять на границе S 2равенствам (7); в частном случае может быть j x= j y= j z= 0 (часть поверхности S 2жестко закреплена). Например, в задаче о равновесии плотины массовая сила – сила тяжести, поверхность S 2подошвы плотины неподвижна, на остальной поверхности S 1действуют силы: напор воды, давление различных надстроек, транспортных средств и т.д.

В общем случае поставленная задача представляет собой пространственную задачу У. т., решение которой трудно осуществимо. Точные аналитические решения имеются лишь для некоторых частных задач: об изгибе и кручении бруса, о контактном взаимодействии двух тел, о концентрации напряжений, о действии силы на вершину конического тела и др. Т. к. уравнения У. т. являются линейными, то решение задачи о совместном действии двух систем сил получается путём суммирования решений для каждой из систем сил, действующих раздельно (принцип линейной суперпозиции). В частности, если для какого-нибудь тела найдено решение при действии сосредоточенной силы в какой-либо произвольной точке тела, то решение задачи при произвольном распределении нагрузок получается путём суммирования (интегрирования). Такие решения, называются Грина функциями, получены лишь для небольшого числа тел (неограниченное пространство, полупространство, ограниченное плоскостью, и некоторые др.). Предложен ряд аналитических методов решения пространственной задачи У. т.: вариационные методы (Ритца, Бубнова – Галёркина, Кастильяно и др.), метод упругих потенциалов, метод Бетти и др. Интенсивно разрабатываются численные методы (конечно-разностные, метод конечных элементов и др.). Разработка общих методов решений пространственной задачи У. т. – одна из наиболее актуальных проблем У. т.