БСЭ БСЭ - Большая Советская Энциклопедия (ФО)

Соч.: Колебания численности промысловых животных, М. – Л., 1935; Снежный покров как фактор среды, его значение в жизни млекопитающих и птиц СССР, М., 1946; О значении структуры снежного покрова в экологии и географии млекопитающих и птиц, в кн.: Роль снежного покрова в природных процессах, М., 1961; Спутник следопыта, 5 изд., М., 1974; Звери, птицы и их взаимосвязи со средой обитания, М., 1976.

Лит.: Насимович А. А., Памяти Александра Николаевича Формозова, «Бюл. Московского общества испытателей природы. Отд. биологический», 1975, т. 80, в. 1 (лит.).

Л. А. Насимович.

Формо'зский проли'в,см. Тайваньский пролив .

Формообразова'ние(биологическое), возникновение и развитие органов, их систем и частей тела организмов; то же, что морфогенез .

Формообразова'ние,образование грамматических форм слова. Ф. противопоставляется словообразованию как соотношение, связывающее формы одного слова (стол – стола, говорю – говорил), а не разные слова одного корня (говорю – переговорю). Решение вопроса о том, какие две формы следует считать формами одного слова, а какие – разными словами (вопроса о границах Ф. и словообразования) зависит от ряда факторов и не всегда однозначно. Часто к одному слову относят формы с одним номинативным (непосредственно отражающим внеязыковую действительность) и разными синтаксическими (отражающими синтаксические возможности словоформ ) значениями, например стол – стола, хожу – ходишь. Формы с разным номинативным значением при этом считаются разными словами и относятся к словообразованию (отучить – отучивать, баня – банщик). Другой подход основывается на противопоставлении грамматических (требующих обязательного выражения) и неграмматических значений. Формы, различающиеся лишь грамматическими значениями, объединяют в одном слове и относят к Ф. (стол – стола, стол – столы, хожу – ходишь, отучить – отучивать), а к словообразованию относят лишь формы, различающиеся неграмматическими значениями (баня – банщик, учить – ученик). Некоторые учёные к Ф. относят формы, способ образования которых регулярен, например англ. наречия на -ly (bright-ly), образующиеся от любого прилагательного. Иногда Ф. понимается в более узком смысле, как относящееся к формам, различающимся номинативными грамматическими значениями (формы числа, вида, каузатива при их грамматическом выражении в языке). В этом случае Ф. занимает промежуточное положение между словообразованием и словоизменением (последнее относится к формам, различающимся лишь синтаксическими значениями).

Лит.: Виноградов В. В., Словообразование в его отношении к грамматике и лексикологии, в его кн.: Исследования по русской грамматике, М., 1975.

В. М. Живов.

Формо'са(Formosa), провинция на С. Аргентины, в Гран-Чако, в междуречье рр. Парагвай, Пилькомайо, Рио-Бермехо. Площадь 72 тыс. км 2 . Население 234 тыс. чел. (1970). Административный центр – г. Формоса. Основные отрасли хозяйства – лесные промыслы и скотоводство. Возделывают главным образом хлопчатник и кукурузу. Производство квебрахового экстракта.

Форм-род(forma-genus), формальный род, родовые названия разрозненных частей ископаемых растений, прижизненная связь которых, как правило, неизвестна. О Ф.-р. говорят также в тех случаях, когда по сохранившейся части трудно судить о систематическом положении исходного растения. В отличие от орган-родов, могут объединять части растений, имеющие лишь внешнее сходство, независимо от их родства.

Фо'рмула(от лат. formula – форма, правило, предписание) (математическая), комбинация математических знаков, выражающая какое-либо предложение; например, суть формулы:

x 3+ y 3< z (1)

2 ´ 2 = 4 (2)

D ABC ~ D EFG (3)

2 ´ 2 = 5 (4)

( a + b ) 2= a 2+ 2 ab + b 2 (5)

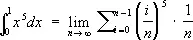, (6)

y’ = y (7)

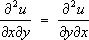(8)

что с помощью Ф. довольно сложные предложения могут быть записаны в компактной и удобной форме (см. Знаки математические ) . Некоторые Ф. [из написанных выше (2), (4), (6)] выражают вполне определённые конкретные суждения и поэтому являются истинными [как (2) и (6)] или ложными [как (4)]. Смысл других Ф. [из написанных выше (1), (3), (5), (7), (8)] зависит от значения входящих в них переменных [например, (1) превращается в истинную Ф. 1 3+ 2 3 < 19 при х = 1, у = 2, z = 19 и в ложную Ф. 3 3+ 4 3< 5 при х = 3, у = 4, z = 5]. Ф. этого типа при таком понимании не являются истинными или ложными непосредственно, но становятся таковыми при замещении переменных конкретными объектами из какой-либо заранее выбранной области. Ф., становящиеся истинными при любом замещении переменных объектами из некоторой области, называются тождественно-истинными в данной области. Например, Ф. (5) тождественно-истинна в области комплексных чисел, ф. (8) тождественно-истинна в области дважды непрерывно-дифференцируемых функций от аргументов x и y . Ф., являющиеся истинными [как (2) и (6)] или тождественно-истинными в какой-либо области [как (5) и (8)], служат для записи математических законов. При этом тождественно-истинные Ф. часто понимаются как утверждения о всеобщности. Например, наиболее распространённое понимание Ф. (5) состоит в том, что она считается сокращённой записью следующего утверждения: «для любых чисел а и b имеет место равенство ( a + b ) 2= a 2+ 2 ab + b 2.

Фо'рмулы хими'ческие,изображения состава химически индивидуальных веществ посредством знаков химических и чисел. В общем случае Ф. х. имеет вид A mB nC p..., где А, В, С... – символы атомов химических элементов, из которых состоит данное вещество; m, n, р – числа, как правило, целые, показывающие, сколько атомов каждого из элементов входит в состав данного вещества (в Ф. х. нестехиометрических соединений они могут быть дробными).

Для установления Ф. х. вещества необходимо: найти его количественный состав в % по массе; заменить процентное содержание по массе отношениями между числами атомов; представить эти отношения целыми числами. Пример: При анализе медного колчедана найдено (в % по массе): 34,64 Cu; 30,42 Fe; 34,94 S. Разделив эти числа на атомные массы Cu (63,55), Fe (55,85), S (32,06), получим частные: 0,545; 0,545; 1,090. Эти числа относятся как 1: 1: 2, откуда искомая Ф. х. – CuFeS 2.