БСЭ БСЭ - Большая Советская Энциклопедия (ФЕ)

К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.

Если зеркало имеет форму эллипсоида вращения, а свет распространяется от одного его фокуса Р к другому Q (причём путь без отражения невозможен), то оптическая длина пути луча PO' + O'Q по свойствам эллипсоида равна всем остальным возможным, например PO'' + О'' Q ; если на пути между теми же точками свет отражается от зеркала меньшей, чем у эллипсоида, кривизны ( MM ) , реализуется минимальный путь, если же большей (зеркало NN ) – максимальный. Условие экстремальности оптической длины пути сводится к требованию, чтобы была равна нулю вариация от интеграла 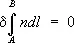(см. Вариационное исчисление ), где А и В – точки, между которыми распространяется свет. Это выражение и представляет собой математическую формулировку Ф. п.

В волновой теории света Ф. п. представляет собой предельный случай Гюйгенса – Френеля принципа и применим, когда можно пренебречь дифракцией света (когда длина световой волны достаточно мала по сравнению с характерными для задачи размерами): рассматривая лучи как нормали к волновым поверхностям, легко показать, что при всяком распространении света оптической длины их путей будут иметь экстремальные значения. Во всех случаях, когда необходимо учитывать дифракцию, Ф. п. перестаёт быть применимым.

Лит.: Fermat P. de, CEuvres, t. 1–4, P., 1891–1912; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики); Крауфорд Ф., Волны, М., 1974 (Берклеевский курс физики, т. 3); Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.

А. П. Гагарин.

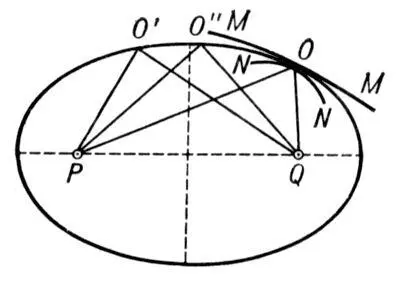
К принципу Ферма: действительный путь света соответствует экстремальному времени распространения.

Ферма'(Fermat) Пьер (17.8.1601, Бомон-де-Ломань, – 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф. его сыном, – «Различные сочинения» (1679); при жизни Ф. полученные им результаты становились известны учёным благодаря переписке и личному общению.

Ф. является одним из создателей теории чисел, где с его именем связаны 2 знаменитые теоремы: Ферма великая теорема и Ферма малая теорема. В области геометрии Ф. в более систематической форме, чем Р. Декарт, развил метод координат, дав уравнения прямой и линий второго порядка и наметив доказательство положения о том, что все кривые второго порядка – конического сечения. В области метода бесконечно малых систематически изучил процесс дифференцирования, дал общий закон дифференцирования степени и применил этот закон к дифференцированию дробных степеней. В подготовке современных методов дифференциального исчисления большое значение имело создание им правила нахождения экстремумов. Ф. дал общее доказательство правильности закона интегрирования степени, подмеченного на частных случаях уже ранее. Он распространил его и на случай дробных и отрицательных степеней. В трудах Ф., таким образом, получили систематическое развитие оба основных процесса метода бесконечно малых, однако он, как и его современники, прошёл мимо связи между операциями дифференцирования и интегрирования. Эта связь была установлена несколько позднее (в систематической форме) Г. Лейбницем и И. Ньютоном. Своими работами Ф. оказал большое влияние на дальнейшее развитие математики. В области физики с именем Ф. связано установление основного принципа геометрической оптики (см. Ферма принцип ) .

Соч.: CEuvres, t. 1–4, P., 1891–1912.

Лит.: Бурбаки Н., Элементы математики, [кн. 8]. Очерки по истории математики, пер. с франц., М., 1963 [лит.]; История математики с древнейших времён до начала XIX столетия, т, 2, М., 1970.

П. Ферма.

Ферма'(франц. ferme, от лат. firmus – крепкий, прочный), несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия зданий, пролётные строения мостов, мачты, опоры линий электропередачи, гидротехнические затворы и др.), а также в качестве несущих конструкций машин и механизмов. По виду материала различают металлические, железобетонные, деревянные и комбинированные (например, металлодеревянные) Ф. Тип Ф. и её очертания ( рис. ) определяются назначением здания или сооружения, видом покрытия, способом опирания Ф. и т.д. Узлы Ф., хотя и считаются шарнирными, практически обладают той или иной степенью жёсткости. При проектировании Ф., как правило, обеспечивается узловое приложение внешней нагрузки (например, прогоны покрытия здания опираются на Ф. в узлах верхнего пояса, балки подвесных кранов крепятся к узлам нижнего пояса и т.д.). Допущения о шарнирном соединении узлов и узловом приложении нагрузки позволяют учитывать при расчёте Ф. только осевые продольные усилия в стержнях (при этом в поперечных сечениях стержней возникают равномерно-распределённые напряжения, позволяющие наиболее эффективно использовать материал). Усилия в стержнях статически определимых плоских Ф. (см. Статически определимая система ) определяют из уравнений статики, пространственных – как правило, путём расчленения на плоские. Статически неопределимые Ф. (см. Статически неопределимая система ) рассчитывают при помощи уравнений метода сил (см. Строительная механика ) , в которых коэффициенты при неизвестных (перемещения) определяют с учётом действия только нормальных усилий в элементах Ф. При расчёте Ф. на подвижные нагрузки используют т. н. линии влияния.

Лит. см. при статьях Строительная механика , Металлические конструкции , Железобетонные конструкции и изделия , Деревянные конструкции .

Л. В. Касабьян.

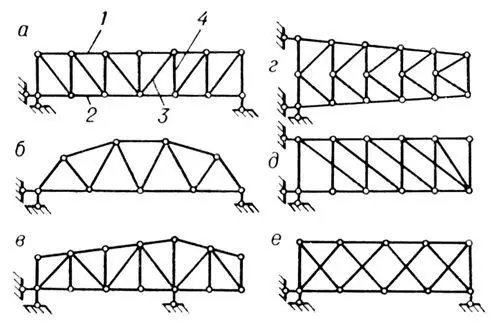
Классификация ферм по типам решётки: а — балочная раскосная; б — балочная с треугольной решёткой; в — балочно-консольная с треугольной решёткой и дополнительными стойками; г — консольная полураскосная; д — консольная двухраскосная; е — балочная двухрешётчатая; 1 — верхний пояс; 2 — нижний пояс; 3 — раскос; 4 — стойка.