БСЭ БСЭ - Большая Советская Энциклопедия (ХИ)

Лит.: Дейч А., Абрар Хидоятов, М. — Л., 1948; Авдеева Л. А., Абрар Хидоятов, Таш., 1960; Фельдман Я., Слово о выдающемся актере, «Театр», 1960, № 2.

Я. С. Фельдман.

А. Хидоятов.

ХидэёсиТоётоми, см. Тоётоми Хидэёси.

Хижа'не,западно-славянское племя, обитавшее в 8—12 вв. на южное побережье Балтийского моря, к В. от г. Росток. Х. входили в племенной союз лютичей .

Хи'йумаа,Хиума, Даго, остров в Моонзундском архипелаге Балтийского моря, в Эстонской ССР. Площадь около 965 км 2 . Высота до 54 м . Сложен главным образом известняками и морскими отложениями антропогена. Почвы щебнистые и песчаные. Сосновые леса, по берегам заросли тростника. Рыболовство и рыбопереработка, земледелие, скотоводство. На Х. — г. Кярдла.

Хика'ят,хикайят (араб. — повествование), литературный термин у народов Ближнего, Среднего Востока и Юго-Восточной Азии. В широком смысле Х. — любое крупное сюжетное прозаическое (реже поэтическое) произведение; в узком значении — жанр безавторского книжного прозаического эпоса (например, «Повесть о ханге Туахе», 17 в., в классической малайской литературе). В арабской, персидской и турецкой литературах термин «Х.» употребляется в значении «рассказ». В турецкой литературе обозначает также анонимный народный рассказ.

«Хи-квадра'т» распределе'ниес f степенями свободы, распределение вероятностей суммы квадратов

c 2 = X 1 2+...+X f 2 ,

независимых случайных величин X 1 ,..., X f , подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция «Х.-к.» р. выражается интегралом

,

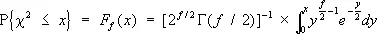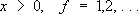
Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы c 2равны соответственно f , 2 f , 8 f . Сумма двух независимых случайных величин c 1 2и c 2 2, с f 1 и f 2 степенями свободы подчиняется «Х.-к.» р. с f 1+ f 2 степенями свободы.

Примерами «Х.-к.» р. могут служить распределения квадратов случайных величин, подчиняющихся Рэлея распределению и Максвелла распределению . В терминах «Х.-к.» р. с чётным числом степеней свободы выражается Пуассона распределение :

.

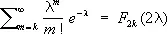Если количество слагаемых f суммы c 2 неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения 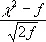сходится к стандартному нормальному распределению:

,

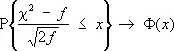где

.

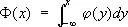
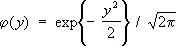Следствием этого факта является другое предельное соотношение, удобное для вычисления F f ( x ) при больших значениях f :

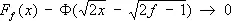
В математической статистике «Х.-к.» р. используется для построения интервальных оценок и статистических критериев. Если Y 1 ,..., Y n — случайные величины, представляющие собой результаты независимых измерений неизвестной постоянной а , причём ошибки измерений Y i — а независимы, распределены одинаково нормально и

Е( Y i — a ) = 0, Е( Y i — а ) 2 = s 2,

то статистическая оценка неизвестной дисперсии s 2выражается формулой

,

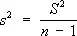где

, .

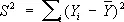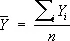Отношение S 2/ s 2подчиняется «Х.-к.» р. с f = n — 1 степенями свободы. Пусть x 1 и x 2 — положительные числа, являющиеся решениями уравнений F f ( x 1 ) = a/2 и F f ( x 2 ) = 1 — a/2 [a —заданное число из интервала (0, 1/ 2)]. В таком случае

Р{ х 1 < S 2/ s 2 < x 2 ) = Р{ S 2/x 2 < s 2< S 2/x 1 } = 1—a.

Интервал ( S 2/x 1 , S 2/x 2 ) называют доверительным интервалом для s 2, соответствующим коэффициенту доверия 1 — a. Такой способ построения интервальной оценки для s 2часто применяется с целью проверки гипотезы, согласно которой s 2= s 0 2(s 0 2— заданное число): если s 0 2принадлежит указанному доверительному интервалу, то делается заключение, что результаты измерений не противоречат гипотезе s 2= s 0 2. Если же

s 0 2£ S 2/x 2 или s 0 2³ S 2/x 1 ,

то нужно считать, что s 2> s 0 2или s 2< s 0 2соответственно. Такому критерию отвечает значимости уровень , равный a.

Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.

Л. Н. Большев.

Хикме'т(Hikmet) Назым, Назым Хикмет Ран (1902—63), турецкий писатель и общественный деятель. См. Назым Хикмет Ран .

Хикме'т Сулейма'н(1889, Басра, — 1968), политический и государственный деятель Ирака. По происхождению турок. Получил образование в Стамбульском университете. В 1925—1933 занимал ряд министерских постов. В 1934 вошёл в национально-патриотическую организацию «Аль-Ахали» (основана в 1931) и стал одним из её лидеров. В октябре 1936, после прихода к власти военной группировки генерала Бакра Сидки, сформировал и возглавил правительство «национальной реформы». Занимал в этом правительстве также пост министра внутренних дел. Правительство Х. С. провозгласило программу национально-демократических преобразований (поощрение национальной промышленности, раздача земель безземельным крестьянам, улучшение системы социального обеспечения и др.) и приступило к её осуществлению. Однако в августе 1937 после выхода из правительства левых членов «Аль-Ахали» и убийства Бакра Сидки Х. С. ушёл в отставку.