БСЭ БСЭ - Большая Советская Энциклопедия (ЦЕ)

Лит.: Протоколы и постановления ЦК Балтийского флота 1917—1918, М., 1963; Балтийские моряки в подготовке и проведении Великой Октябрьской социалистической революции. [Сб. док-тов], М., 1957; Измайлов Н. Ф., Пухов А. С., Центробалт, 2 изд., Калининград, 1967.

Центробе'жная му'фта,см. Муфта.

Центробе'жная си'ла,сила, с которой движущаяся материальная точка действует на тело (связь), стесняющее свободу движения точки и вынуждающее её двигаться криволинейно. Численно Ц. с. равна mv 2/ r , где m — масса точки, v — её скорость, r — радиус кривизны траектории, и направлена по главной нормали к траектории от центра кривизны (от центра окружности при движении точки по окружности). Ц. с. и центростремительная сила численно равны друг другу и направлены вдоль одной прямой в противоположные стороны, но приложены к разным телам — как силы действия и противодействия. Например, при вращении в горизонтальной плоскости привязанного к верёвке груза центростремительная сила действует со стороны верёвки на груз, вынуждая его двигаться по окружности, а Ц. с. действует со стороны груза на верёвку, натягивает её и при достаточно большой скорости движения может оборвать.

При применении к решению задач динамики Д'Аламбера принципа термину «Ц. с.» придают иногда др. смысл и называют Ц. с. составляющую силы инерции материальной точки, направленную по главной нормали к траектории. Изредка Ц. с. называют также нормальную составляющую переносной силы инерции при составлении уравнений относительного движения.

Центробе'жное литьё,см. Литьё центробежное.

Центробе'жное модели'рование,метод моделирования физического, применяемый для научных исследований и изучения на моделях свойств (характеристик) инженерных сооружений, находящихся под действием сил тяжести. Чаще всего Ц. м. пользуются при изучении сооружений из грунта или сооружений, взаимодействующих с грунтом (откосы, насыпи, плотины, фундаменты, подземные сооружения и др.). Цель исследований — определение возникающих в сооружении деформаций и напряжений, т. е. условий, при которых сооружению не грозит разрушение, или установление причин и характера разрушений и т.п.

Методами Ц. м. можно изучать действие на людей и объекты техники перегрузок, возникающих при авиационных и космических полётах (см. Космического полёта имитация ) . Идею Ц. м. можно также использовать для создания на борту космического летательного аппарата искусственной «тяжести» (см. Невесомость ) .

При моделировании необходимо выполнение подобия критериев. Когда основная нагрузка на сооружение обусловлена действием сил тяжести, а модель изготовлена из того же материала, что и натура, этот критерий имеет вид

g 1l 1 = gl, (1)

где g и / — ускорение силы тяжести и линейный размер натуры соответственно, g 1— «модельное» ускорение и l 1— линейный размер модели. Т. к. обычно модель меньше натуры, т. е. L 1 < l, то для модели необходимо обеспечить условия, при которых g 1 > g. Такие условия можно приближённо создать, поместив модель в центробежную машину (центрифугу). В этом и состоит идея Ц. м.

В центрифуге камера вместе с находящейся в ней моделью вращается вокруг вертикальной оси с угловой скоростью w. При этом на каждую частицу модели действует центробежная сила, направленная от оси вращения и равная m кh kw 2, где m к— масса частиц, h k— её расстояние от оси вращения. Размеры центрифуги делают такими, чтобы расстояния h k были велики по сравнению с размерами модели. Тогда можно приближённо принять все h k = h, где h — расстояние от оси вращения центра тяжести модели, и считать действующие на частицы модели силы равными m кhw 2, т. е. аналогичными силам тяжести m kg 1, где g 1 = h w 2. В результате условие (1) примет вид

h ( 2l 1 = gl или w 2= gl/l 1h. (2)

Отсюда определяется значение угловой скорости, при которой для модели данного размера можно осуществить Ц. м. (чем меньше l 1, тем больше должна быть w).

Если модель и натура выполнены из материалов с разными плотностями и разными прочностными характеристиками, определяемыми, например, модулем упругости (модулем Юнга) Е, то критерий подобия изменится и Ц. м. будет возможно, когда

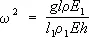. (3)

При Ц. м. движения тел в воде вблизи её поверхности или процессов формирования и движения волн применяют кольцевой лоток, выполненный в форме замкнутого кольца, заполненный водой и вращающийся вокруг вертикальной оси, проходящей через центр кольца. При таком Ц. м. могут совместно выполняться подобия критерии Рейнольдса и Фруда.

Идея Ц. м. в общем виде высказана французским учёным Э. Филлипсом (1869); в СССР детально разработана и применена Г. И. Покровским и И. С. Федоровым (1932).

Лит.: Покровский Г. И., Федоров И. С., Центробежное моделирование в строительном деле, М., 1968; их же, Центробежное моделирование в горном деле, М., 1969; Рамберг Х., Моделирование деформаций земной коры с применением центрифуги, пер. с англ., М., 1970.

Г. И. Покровский.

Центробе'жные не'рвные воло'кна,эфферентные, моторные нервные волокна, отростки нервных клеток ( аксоны ) вместе с их оболочками, передающие возбуждение от центральной нервной системы к рабочим органам (мышцам, железам). Различают черепномозговые, спинномозговые и др. Ц. н. в. Они могут относиться как к соматическим, так и к вегетативным отделам нервной системы. Среди периферических нервов только некоторые истинно центробежные, большинство же периферических нервов являются смешанными, т. е. включают в себя и центростремительные нервные волокна. В составе одного нерва центробежные волокна нередко проходят к разным рабочим органам. По скорости проведения возбуждения Ц. н. в. делятся на 3 группы: А, В, С с несколькими подгруппами. К группе А относятся наиболее быстропроводящие волокна, иннервирующие скелетные мышцы. Парасимпатические и симпатические волокна, проводящие возбуждение с меньшей скоростью, относятся к волокнам групп В и С. См. также Нервные волокна.

Центробе'жный вентиля'тор, см. Вентилятор.

Центробе'жный компре'ссор,см. Компрессор.