БСЭ БСЭ - Большая Советская Энциклопедия (ЧЕ)

Наиболее многочисленны работы Ч. в области математического анализа. Ему была, в частности, посвящена диссертация на право чтения лекций, в которой Ч. исследовал интегрируемость некоторых иррациональных выражений в алгебраических функциях и логарифмах. Интегрированию алгебраических функций Ч. посвятил также ряд других работ. В одной из них (1853) была получена известная теорема об условиях интегрируемости в элементарных функциях дифференциального бинома. Важное направление исследований по математическому анализу составляют его работы по построению общей теории ортогональных многочленов. Поводом к её созданию явилось параболическое интерполирование способом наименьших квадратов. К этому же кругу идей примыкают исследования Ч. по проблеме моментов и по квадратурным формулам. Имея в виду сокращение вычислений, Ч. предложил (1873) рассматривать квадратурные формулы с равными коэффициентами (см. Приближённое интегрирование ). Исследования по квадратурным формулам и по теории интерполирования были тесно связаны с задачами, которые ставились перед Ч. в артиллерийском отделении военно-учёного комитета.

Ч. — основоположник т. н. конструктивной теории функций, основной составляющий элемент которой — теория наилучшего приближения функций (см. Приближение и интерполирование функций , Чебышева многочлены ) . Простейшая постановка задачи Ч. такова (1854): дана непрерывная функция f ( x ); среди всех многочленов степени n найти такой Р ( х ), чтобы в данном промежутке [ a , b ] выражение

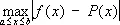
было возможно меньшим.

Помимо указанного равномерного наилучшего приближения, Ч. рассматривал также квадратическое приближение, а помимо приближений алгебраическими многочленами, — приближение посредством тригонометрических полиномов и с помощью рациональных функций.

Теория машин и механизмов была одной из тех дисциплин, которыми Ч. систематически интересовался всю жизнь. Особенно многочисленны его работы, посвященные синтезу шарнирных механизмов, в частности параллелограмму Уатта (1861, 1869, 1871, 1879 и др.). Большое внимание он уделял конструированию и изготовлению конкретных механизмов. Интересны, в частности, его стопоходящая машина, имитирующая движение животного при ходьбе, а также автоматический арифмометр. Изучение параллелограмма Уатта и стремление усовершенствовать его натолкнуло Ч. на постановку задачи о наилучшем приближении функций (см. выше). К прикладным работам Ч. относится также оригинальное исследование (1856), где он поставил задачу найти такую картографическую проекцию данной страны, сохраняющую подобие в малых частях, чтобы наибольшее различие масштабов в разных точках карты было наименьшим. Ч. высказал без доказательства мнение, что для этого отображение должно сохранять на границе постоянство масштаба, что впоследствии и было доказано Д. А. Граве.

Ч. оставил яркий след в развитии математики и собственными исследованиями, и постановкой соответствующих вопросов перед молодыми учёными. Так, по его совету А. М. Ляпунов начал цикл исследований по теории фигур равновесия вращающейся жидкости, частицы которой притягиваются по закону всемирного тяготения.

Труды Ч. ещё при жизни нашли широкое признание не только в России, но и за границей; он был избран член Берлинской АН (1871), Болонской АН (1873), Парижской АН (1874; член-корреспондент 1860), Лондонского королевского общества (1877), Шведской АН (1893) и почётным член многих других русских и иностранных научных обществ, академий и университетов.

В честь Ч. АН СССР учредила в 1944 премию за лучшие исследования по математике.

Соч.: Сочинения, т. 1—2, СПБ. 1899—1907; Полн. собр. соч., т. 1—5, М.—Л., 1944—1951 (лит.); Избр. труды, М., 1955.

Лит.: Ляпунов А. М., Пафнутий Львович Чебышев, в кн.: Чебышев П. Л., Избр. математические труды, М.—Л., 1946; Стеклов В. А., Теория и практика в исследованиях Чебышева. Речь..., П., 1921; Крылов А. Н., Пафнутий Львович Чебышев. Биографический очерк, М.—Л., 1944; Научное наследие П. Л. Чебышева, в. 1—2, М.—Л., 1945; Делоне Б. Н., Петербургская школа теории чисел, М.—Л., 1947 (лит.).

Б. В. Гнеденко.

П. Л. Чебышев.

Чебыше'ва многочле'ны,

1) Ч. м. 1-го рода — специальная система многочленов последовательно возрастающих степеней. Для n = 0, 1, 2,... определяются формулой:

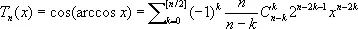
В частности, Т 0 = 1; T 1= х ; T 2= 2 x 2¾1; T 3= 4 x 3¾ 3 x ; T 4= 8 x 4 ¾ 8 x 2+ 1. Ч. м. T n ( x ) ортогональны (см. Ортогональные многочлены ) на отрезке [—1; + 1] относительно веса (1 — x 2) ¾1/2. Дифференциальное уравнение:

(1 — x 2) у" — ху + n 2 у = 0 .

Рекуррентная формула: T n+ 1( x ) = 2xTn ( х ) - T n ¾1( x ) .

Ч. м. 1-го рода являются частным случаем Якоби многочленовP n ( ab)( x ) :

.

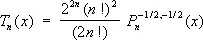2) Ч. м. 2-го рода U n ( x ) — ортогональная на отрезке [—1; + 1] относительно веса (1 — x 2) 1/2система многочленов, связанная с Ч. м. 1-го рода, например рекуррентным соотношением:

(1 — x 2) U n ¾1( х ) = xTn ( х ) ¾ T n+ 1( х ) .

Лит.: Чебышев П. Л., Полн. собр. соч., т. 2—3, М.—Л., 1947—48; Сеге Г., Ортогональные многочлены, пер. с англ., М., 1962.

Чебыше'ва нера'венство,

1) одно из основных неравенств для монотонных последовательностей или функций. В случае конечных последовательностей

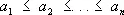
и

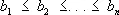
оно имеет вид:

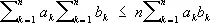
а в интегральной форме ¾ вид:

,

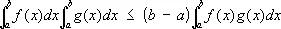где f ( x ) ³ 0, g ( x ) ³ 0 и обе функции либо убывают, либо возрастают. Ч. н. установлено П. Л. Чебышевым (1882).

2) Неравенство, дающее оценку вероятности того, что отклонение случайной величины от её математического ожидания превзойдёт некоторую заданную границу. Пусть x — какая-либо случайная величина, Ex = a — её математическое ожидание, а Dx = s 2¾ её дисперсия. Тогда Ч. н. утверждает, что вероятность неравенства | x ¾ a |³ k s не превосходит величины 1 /k 2 . Если x — сумма независимых случайных величин, то при некоторых дополнительных ограничениях оценка 1 /k 2может быть заменена оценкой