БСЭ БСЭ - Большая Советская Энциклопедия (ШР)

где R — газовая постоянная; D Н плпринимается постоянной в интервале Т пл— Т. Строгое применение Ш. у. ограничено идеальными растворами. Построив по Ш. у. кривые температурной зависимости растворимости для твёрдой фазы каждого из компонентов двойной системы, можно найти эвтектическую точку (см. Эвтектика ) и получить растворимости диаграмму .

Ш. у. выведено в 1890 И. Ф. Шредером. Оно известно также под названием «логарифмики Шредера» и уравнения Шредера — Ле Шателье (А. Ле Шателье ранее получил зависимость растворимости от температуры в дифференциальной форме, на основании которой в 1894 вывел уравнение, аналогичное Ш. у.).

Лит.: Кипнис А. Я., Развитие химической термодинамики в России, М.—Л., 1964. См. также лит. при ст. Растворы .

М. Х. Карапетьянц.

Шрёдер-Деврие'нт(Schröder-Devrient, урожд. Шрёдер) Вильгельмина (6.12.1804, Гамбург, — 26.1.1860, Кобург), немецкая певица (сопрано). Пению училась у Ю. Моцатти в Вене. В 1821 дебютировала в партии Памины («Волшебная флейта» Моцарта). Гастролировала в городах Италии, в Париже, Лондоне, Праге. Исполнила партию Леоноры («Фиделио» Бетховена, 1822, Вена), которая принесла ей славу выдающейся певицы Европы. В 1823—47 солистка придворной оперы в Дрездене. За участие в Дрезденском восстании 1849 была выслана из Саксонии и не выступала до 1856. Гастролировала в России. В искусстве Ш.-Д. сочеталось вокальное мастерство с большой драматической одарённостью. Среди лучших партий: Сента («Летучий голландец» Вагнера), Агата («Вольный стрелок» Вебера).

Лит.: Серов А. Н., Критические статьи, т. 3, СПБ, 1893, с. 1361—75; Wolzogen Avon, Wilhelmine Schröder-Devrient, Lpz., 1863; Hagemann K., Wilhelmine Schröder-Devrient, Wiesbaden, 1947.

Шрёдингер(Schrödinger) Эрвин (12.8.1887, Вена, — 4.1.1961, там же; похоронен в Альпбахе, Тироль), австрийский физик, один из создателей квантовой механики. Окончил Венский университет (1910). С 1911 работал в Физическом институте Венского университета. В 1920 профессор Высшей технической школы в Штутгарте, в 1921 — Высшей технической школы в Бреслау (Вроцлаве), в 1921—27 — Высшей технической школы в Цюрихе, с 1927 профессор Берлинского университета. В 1933—35 профессор Оксфордского университета, в 1936—38 — университета в Граце, в 1938—39 — в Генте, с 1940 профессор Королевской академии в Дублине, затем директор основанного им Института высших исследований. С 1956 профессор Венского университета. Основные труды по математической физике, теории относительности, физике атома и биофизике. К ранним работам Ш. относятся исследования по теории кристаллической решётки и создание в 1920 математической теории цвета, которая легла в основу современной колориметрии. Важнейшей заслугой Ш. является создание им волновой механики (конец 1925 — начало 1926): исходя из гипотезы Л. де Бройля о волнах материи, он показал, что стационарные состояния атомных систем могут рассматриваться как собственные колебания волнового поля, соответствующего данной системе; Ш. нашёл основное уравнение нерелятивистской квантовой механики ( Шрёдингера уравнение ) и дал его решение для ряда частных задач, а также общий метод его применения в теории возмущений. Установил связь волновой механики с «матричной механикой» В. Гейзенберга, М. Борна и П. Йордана и доказал их физическую тождественность. Развитый Ш. математический формализм и введённая им волновая функция y явились наиболее адекватным математическим аппаратом квантовой механики и её применений. Нобелевская премия (1933). Иностранный член АН СССР (1934).

Соч.: Abhandlungen zur Wellenmechanik, 2 Aufl., Lpz., 1928; в рус. пер. — Избр. труды по квантовой механике, М., 1976 (сер. «Классики науки»); Что такое жизнь? С точки зрения физика, 2 изд., М., 1972.

Л. С. Полак.

Э. Шрёдингер.

Шрёдингера уравне'ние,основное динамическое уравнение нерелятивистской квантовой механики ; названо в честь австрийского физика Э. Шрёдингера , который предложил его в 1926. В квантовой механике Ш. у. играет такую же фундаментальную роль, как уравнение движения Ньютона в классической механике и Максвелла уравнения в классической теории электромагнетизма. Ш. у. описывает измерение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая функция y в начальный момент времени, то, решая Ш. у., можно найти y в любой последующий момент времени t.

Для частицы массы т , движущейся под действием силы, порождаемой потенциалом V ( х , у , z , t ), Ш. у. имеет вид:

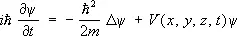, (1)

где i = 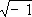, 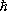= 1,05 .10 ¾27 эрг . сек — Планка постоянная , 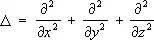— Лапласа оператор ( х , у , z — координаты). Это уравнение называется временны'м Ш. у.

Если потенциал V не зависит от времени, то решения Ш. у. можно представить в виде:

y( х , у , z , t ) = 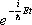y ( х , у , z ), (2)

где Е — полная энергия квантовой системы, а y ( x , у , z ) удовлетворяет стационарному Ш. у.:

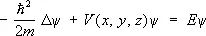(3)

Для квантовых систем, движение которых происходит в ограниченной области пространства, решения Ш. у. существуют только для некоторых дискретных значений энергии: E 1 , E 2 , ... , E n ,...; члены этого ряда (в общем случае бесконечного) нумеруются набором целых квантовых чисел n. Каждому значению Е п соответствует волновая функция y n ( x , у , z ), и знание полного набора этих функций позволяет вычислить все измеримые характеристики квантовой системы.

В важном частном случае кулоновского потенциала

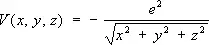
(где е — элементарный электрический заряд) Ш. у. описывает атом водорода, и E n представляют собой энергии стационарных состояний атома.

Ш. у. является математическим выражением фундаментального свойства микрочастиц — корпускулярно-волнового дуализма , согласно которому все существующие в природе частицы материи наделены также волновыми свойствами (эта гипотеза впервые была высказана Л. де Бройлем в 1924). Ш. у. удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, содержит описание движения частиц по законам классической механики. Переход от Ш. у. к классическим траекториям подобен переходу от волновой оптики к геометрической. Аналогия между классической механикой и геометрической оптикой, которая является предельным случаем волновой, сыграла важную роль в установлении Ш. у.