БСЭ - Большая Советская энциклопедия (Пр)

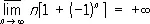
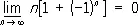
Последовательность имеет конечный или бесконечный П. тогда и только тогда, когда её верхний П. совпадает с нижним, при этом их общее значение и является её П. Конечный верхний П. последовательности можно также определить как такое число а, что при любом e > 0 существует бесконечно много членов последовательности, больших, чем а — e, и лишь не более, чем конечное число членов, больших, чем a + e .

Предел функции. Пусть функция f , принимающая действительные значения, определена в некоторой окрестности точки x 0, кроме, быть может, само'й точки x 0. Функция f имеет П. в точке x 0, если для любой последовательности точек x n, n = 1, 2,..., x n ¹ x 0, стремящейся к точке x 0, последовательность значений функции f ( x n ) сходится к одному и тому же числу А, которое и называется пределом функции f в точке x 0, (или при x ® x 0 ) при этом пишется

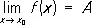
или

f ( x ) ® A при x ® x 0

В силу этого определения на П. функций переносятся свойства П. суммы, произведения и частного последовательностей, а также сохранение неравенств при предельном переходе.

Определение П. функции можно сформулировать и не прибегая к понятию П. последовательности: число А называется пределом функции f в точке x 0, если для любого числа e > 0 существует такое число d > 0, что для всех точек х ¹ x 0, удовлетворяющих условию ½ х — x 0 ½ < d , x ¹ x 0, выполняется неравенство ½ f ( x ) — A½ < e.

Все основные элементарные функции: постоянные, степенная функция х a , показательная функция a x, тригонометрические функции sin x, cos x, tg x и ctg x и обратные тригонометрические функции arcsin x, arccos x, arctg x и arcctg x во всех внутренних точках своих областей определения имеют П., совпадающие с их значениями в этих точках. Но это не всегда бывает так. Функция

,

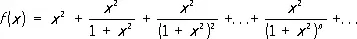являющаяся суммой бесконечной геометрической прогрессии со знаменателем q = 1/(1 + x 2 ) , 0 < q < 1 , в точке х = 0 имеет П., равный 1, ибо f ( x ) = 1 + x 2 при x ¹ 0 . Этот П. не совпадает со значением функции f в нуле: f (0) = 0. Функция же

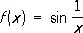, x ¹ 0,

вовсе не имеет П. при х ® 0 , ибо уже для значений x n = 1 / (p/2 + p n ) последовательность соответствующих значений функции f ( x n ) = ( - 1) n не имеет П.

Если П. функции при х ® х 0 равен нулю, то она называется бесконечно малой при х ® х 0. Например, функция sin x бесконечно мала при х ® 0 . Для того чтобы функция f имела при х ® х 0 П., равный А, необходимо и достаточно, чтобы f ( x ) = A + a( x ) , где a( х ) является бесконечно малой при х ® х 0

Если при определении П. функции f в точке x 0 рассматриваются только точки х, лежащие левее (правее) точки x 0, то получающийся П. называется пределом слева (справа) и обозначается 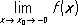(соответственно ).

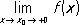Функция имеет П. в некоторой точке, если её П. слева в этой точке равен её П. справа. Понятие П. функции обобщается и на случай, когда аргумент стремится к бесконечности:

, ,

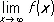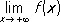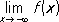
Например,

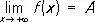
означает, что для любого e > 0 существует такое d > 0, что для всех х, удовлетворяющих условию x > d, выполняется неравенство ½ f ( x ) - А½ < e.

Примером функций, всегда имеющих П., являются монотонные функции . Так, если функция f определена на интервале ( а, b ) и не убывает, то в каждой точке х, а < х < b, она имеет конечный П. как слева, так и справа; в точке в П. справа, который конечен тогда и только тогда, когда функция f ограничена снизу, а в точке b П. слева, конечный в том и только в том случае, когда функция ограничена сверху. В общем же случае стремление к П. может носить разный, необязательно монотонный характер. Например, функция f ( x ) = x 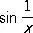при х ® 0 стремится к нулю, бесконечное число раз переходя от возрастания к убыванию и обратно.

Т. н. внутренний критерий (критерий Коши) существования П. функции в точке состоит в следующем: функция f имеет в точке x 0 П. в том и только в том случае, если для любого e > 0 существует такое d > 0, что для всех точек х' и х'', удовлетворяющих условию ½ х’ - x 0 ½ < d, ½ x'' — x 0 ½ < d, x' ¹ x 0 , x'’ ¹ x 0, выполняется неравенство ½ f ( x'' ) — f ( x' )½ < e.

Для функций, как и для последовательностей, определяются понятия бесконечных П. вида 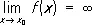, , 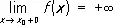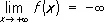и т.д.; в этих случаях функция f называется бесконечно большой при х ® х 0, При х ® х 0 + 0 или При х ® +¥ соответственно и т.д. Например,

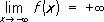
означает, что для любого e > 0 существует такое d > 0, что для всех х, удовлетворяющих условию х < -d, выполняется неравенство f ( x ) > e .

Расширение понятия предела функции. Если функция f определена на некотором множестве Е числовой прямой и точка x 0 такова, что в любой её окрестности имеются точки множества Е, то аналогично данному выше определению П. функции, заданной в некоторой окрестности точки x 0, кроме, быть может, самой точки x 0, определяется понятие предела функции по множеству Е