Евгений Сидоркин - КНИГА-ТРЕНАЖЕР: «Базовая подготовка к ЕГЭ по информатике в компьютерной форме». Авторский курс

Решение:

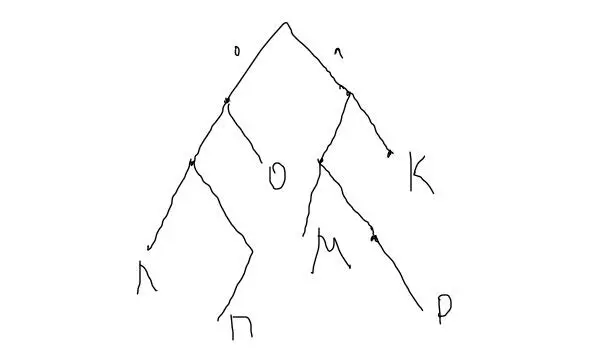
Изобразим буквы К, Л, П, Р на дереве (рекомендую на экзамене прямо так и рисовать мышкой, как у меня выше нарисовано). По условию задачи необходимо, чтобы слово не являлось началом другого кодового слово, т.к. необходимо, чтобы выполнялось прямое условие Фано. Необходимо поставить в дерево две буквы: О и М, чтобы условие Фано выполнялось. Как это сделать? Т.к. буква О в слове «молоко» встречается 3 раза, то мы поставим эту букву на меньшую глубину дерева (01), чтобы получить наименьший код. Букву М, которая встречается всего 1 раз, поставим на большую глубину дерева (100). Итого имеем следующие длины: М=100=3, О=01=2*3 (т.к. 3 раза встречается, поэтому умножаем на 3) =6, Л=000=3, К=11=2. Длина кода равна=3+6+3+2=14.

Ответ: 14.

Рассмотрим задачу на обратное условие Фано.

Пример 4.2

По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г. Для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б используются такие кодовые слова: А: 00011, Б: 1001, В: 01100. Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.

Решение:

Для выполнения прямого условия Фано букву Г мы можем поставить на свободную ветку дерева, то Г=11 (кратчайший путь), т.к. этот путь не будет являться ничьим началом кодового слова. При обратном условии Фано букву Г=10 можем поставить (кратчайший путь), т.к. 10 не является окончанием ни одного из приведенных кодовых слов в условии. Г=00 взять не можем, т.к. 00 является окончанием В, и тогда не выполняется обратное условие Фано. Из двух чисел 11 и 10 наибольшее – 11.

Ответ : 11.

Пример 4.3

Для передачи данных по каналу связи используется 5битовый код. Сообщение содержит только буквы А, Б и В, которые кодируются следующими кодовыми словами: А – 11010, Б – 10111, В – 01101. При передаче возможны помехи. Однако некоторые ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов отличаются друг от друга не менее чем в трёх позициях. Поэтому если при передаче слова произошла ошибка не более чем в одной позиции, то можно сделать обоснованное предположение о том, какая буква передавалась. (Говорят, что «код исправляет одну ошибку». ) Например, если получено кодовое слово 10110, считается, что передавалась буква Б. (Отличие от кодового слова для Б только в одной позиции, для остальных кодовых слов отличий больше.) Если принятое кодовое слово отличается от кодовых слов для букв А, Б, В более чем в одной позиции, то считается, что произошла ошибка (она обозначается «х»). Получено сообщение 11000 11101 10001 11111. Декодируйте это сообщение – выберите правильный вариант.

1) АххБ 3) хххх

2) АВхБ 4) АВББ

Решение:

Декодируем каждое слово сообщения. Первое слово: 11000 отличается от буквы А только одной позицией, поэтому на первом месте будет А. Второе слово: 11101 отличается от буквы В только одной позицией, поэтому на второй позиции будет В. Третье слово: 10001 отличается от любой буквы более чем одной позицией, поэтому третья позиция – x. Четвёртое слово: 11111 отличается от буквы Б только одной позицией, поэтому четвертая позиция – Б. Таким образом, ответ: АВхБ.

Ответ : 2.

Задачи для самостоятельного решения

Задача 4.4

По каналу связи передаются сообщения, содержащие только четыре буквы: М, А, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: М – 101, Р – 100, Т – 01. Укажите кодовое слово минимальной длины, которое можно использовать для буквы А. Если таких кодовых слов несколько, приведите кодовое слово с минимальным числовым значением.

Примечание. Условие Фано означает, что соблюдается одно из двух условий: либо никакое кодовое слово не является началом другого кодового слова, либо никакое кодовое слово не является окончанием другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

Задача 4.5

По каналу связи передаются сообщения, содержащие только шесть букв: Я, Н, В, А, Р, Ь. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Н – 00, В – 01, Р – 10, Ь – 111. Укажите минимально возможную длину закодированной последовательности для слова ВАРВАР.

Алгоритм – это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность.

Алгоритм можно задать одним из следующих способов:

• словесное описание последовательности действий на

естественном языке;

• графическое изображение в виде блок-схемы;

• запись при помощи псевдокода (алгоритмического

языка);

• запись на языке программирования.

В этом типе задач рассматривается в основном словесное описание алгоритмов на естественном языке, а потому никаких специальных знаний для решения задачи не требуется. В данных типах задач используются разные исполнители – от чертежника, черепашки до автомата. Рассмотрим основные типы задач, которые здесь могут быть использованы.

Пример 5.1

Алгоритм получает на вход натуральное число N и строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.

2. Складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления суммы на 2.

3. Предыдущий пункт повторяется для записи с добавленной цифрой.

4. Результат переводится в десятичную систему.

Пример. Дано число N = 13. Алгоритм работает следующим образом:

1. Двоичная запись числа N: 1101.

2. Сумма цифр двоичной записи 3, остаток от деления на 2 равен 1, новая запись 11011.

3. Сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110.

4. Результат работы алгоритма R = 54.

При каком наименьшем числе N в результате работы алгоритма получится R> 170? В ответе запишите это число в десятичной системе счисления.

Решение : Рассмотрим первое попавшееся число, которое больше 170. 171=10101011. У этого числа отделим последние два разряда 171= 101010 | 11 не походит, т.к., выполняя второе правило, алгоритм сложит все единицы, которые стоят слева от вертикальной линии 1+1+1=3, а затем 3 разделим на 2 без остатка и получим 1 и запишем эту единица справа от числа 101010 1. Затем снова применим второе правило к получившемуся числу 101010 | 1. И получим уже новое число 101010 | 10. Получившееся число 10101010=170 по условию задачи должно быть равно 171. Понятно, что 171 не равно 170, поэтому число 171 не подходит. Берем число 172=10101100. Проверяем его на второе правило 2 раза и видим, что число 172 подходит. Осталось только число 10101100 без двух правых нулей перевести в десятичную систему счисления. Получаем 101011=43.