Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

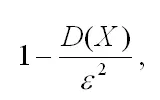
т. е.

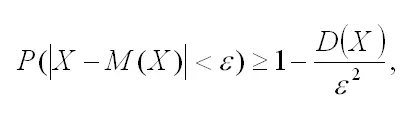
Доказательство. Так как события |Х-М(Х)|‹ε и |Х-М(Х)|≥ ε являются противоположными, то на основании теоремы сложения вероятностей сумма их вероятностей равна единице:

P(|Х-М(Х)|‹ ε )+P(|Х-М(Х)| ≥ε )=1.

Выразим из полученного равенства вероятность | Х-М(Х)|‹ ε :

P(|Х-М(Х)|‹ ε )=1– P(|Х-М(Х)| ≥ε ). (1)

Дисперсия случайной величины Х определяется по формуле:

D(X)=(x1–M(X))2*p1+(x2–M(X))2*p2+…+(xn–M(X))2*pn.

Если отбросить первые k+1 слагаемые, для которых выполняется условие |xj-M(X)|‹ ε , то получим следующее неравенство:

D(X)≥(xk+1–M(X))2*pk+1+(xk+2–M(X))2*pk+2+…+(xn–M(X))2*pn.

Возведя обе части неравенства

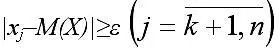
в квадрат, получим равносильное неравенство |xj–M(X)|2≥ε2 . Если заменить в оставшейся сумме каждый из множителей |xj–M(X)|2 числом β2 , то получим следующее выражение:

D(X)≥ ε2(pk+1+ pk+2+…+ pn).

Так как сумма в скобках (pk+1+ pk+2+…+ pn) является выражением вероятности P(|Х-М(Х)| ≥ε ) , то справедливо неравенство (2):

D(X)≥ ε2P(|Х-М(Х)|≥ε),

или

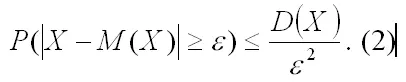
Если подставить неравенство (2) в выражение (1), то получим:

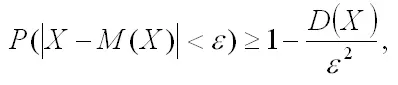
что и требовалось доказать.

Теорема Чебышева.Если величины X1, X2, …, Xn являются последовательностью попарно независимых случайных величин, имеющих дисперсии, ограниченные одной и той же постоянной С (D(Xi)≤C), то, как бы ни было мало положительное число ε , вероятность неравенства

ε будет приближаться к единице, если число случайных величин достаточно мало. Другими словами, для любого положительного числа существует предел:

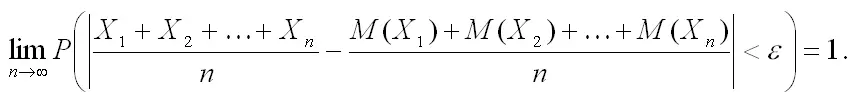
Доказательство. В силу второго свойства дисперсии (постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат) и оценки D(Xi)≤C получим:

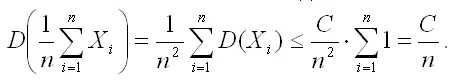
Таким образом,

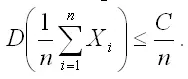
Из данного соотношения и неравенства Чебышева вытекает, что

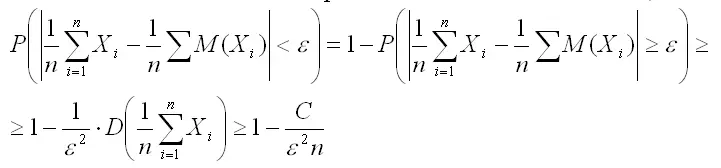
Отсюда, переходя к пределу при n› ε , получим

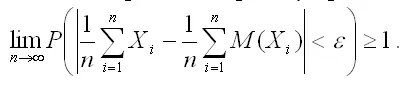
Учитывая, что вероятность не может быть больше единицы, окончательно запишем:

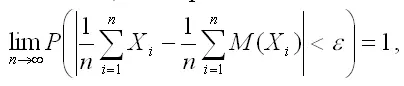
что и требовалось доказать.

Если для рассматриваемых случайных величин математическое ожидание одинаково и дисперсии данных величин ограничены, то к ним применима теорема Чебышева. В этом случае считается справедливым утверждение, что среднее арифметическое достаточно большого количества попарно независимых случайных величин, дисперсии которых ограничены одной и той же постоянной, утрачивает характер случайной величины.

Предположим, что проводится n независимых испытаний. В каждом из этих испытаний вероятность наступления события А постоянна и равна р . Задача состоит в определении относительной частоты появлений события А . Данная задача решается с помощью теоремы Бернулли.

Теорема Бернулли.Если в каждом из n независимых испытаний событие A имеет постоянную вероятность p , то, как угодно близка к единице вероятность того, что отклонение относительной частоты m/n от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, т. е. при соблюдении условий теоремы справедливо равенство:

Доказательство. Предположим, что

является дискретной случайной величиной, которая характеризует число появлений события А в каждом из испытаний. Данная величина может принимать только два значения: 1 (событие А наступило) с вероятностью р и 0 (событие А не наступило) с вероятностью q=1-p .

Случайные дискретные величины Хi являются попарно независимыми и дисперсии их ограниченны, следовательно, к данным величинам применима теорема Чебышева:

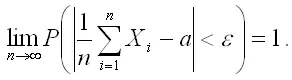
Математическое ожидание а каждой из величин Хi равно вероятности р наступления события, следовательно, справедливо следующее равенство:

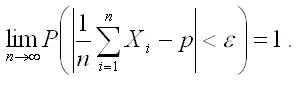
Таким образом, необходимо доказать, что дробь

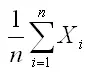
или

равна относительной частоте m/n появлений события А в n испытаниях.

Каждая из величин

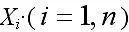
при наступлении события А в соответствующем испытании принимает значение, равное единице. Следовательно, сумма

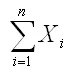
равна числу m появлений события А в n испытаниях:

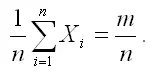
С учётом данного равенства можно окончательно записать:

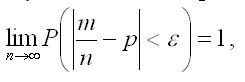
что и требовалось доказать.