Александр Матанцев - Пирамиды – источники огромной энергии по древним технологиям и возможности сейчас

Как же заставить вибрировать каменный массив весом 5 273 834 тонн? На первый взгляд эта задача представляется невыполнимой. Тем не менее не так давно на Земле жил человек, который утверждал, что ему это по силам! Никола Тесла, физик и изобретатель, обладатель болле шестисот патентов, создал устройство, названное им «сейсмическая машина». Он утверждал, что способен разрушить здание при помощи колебаний, частота которых совпадает с резонансной частотой указанного здания. Ученый Том Берден в научном докладе, представленном в 1988 году в международное общество Тесла, пошел дальше Теслы в изучении Земли как источника энергии и предложил, что «для получения огромной энергии всего-то и надо, что запустить в недра Земли „сетчатый сигнал“ и получить в ответ „пластинчатый сигнал“. Стоячая S-волна постоянно пополняется за счет сейсмической энергии из Земли, поэтому энергию можно черпать постоянно».

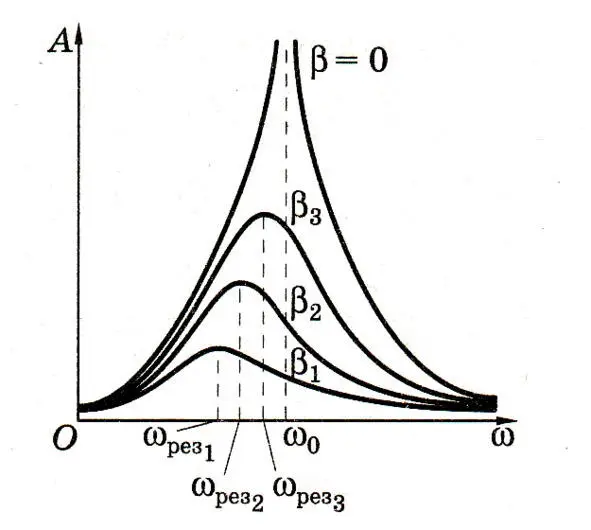
Рис. 30. Резонансные кривые [52]

Резонансные кривые отличаются друг от друга амплитудой и формой – рис. 30. Изменение резонансной частоты зависит от среды, или от материала пирамиды, определяемого коэффициентом β. В свою очередь этот коэффициент связан с добротностью, при β=0, добротность максимальна. Реально, в пирамиде применены слои из разных материалов: известняка, песчаника, гранита и других. Если нужно увеличить или уменьшить резонансную частоту, то можно подобрать нужный материал. Каждая из резонансных кривых обладает своим коэффициентом затухания и добротностью. Чем выше добротность, тем уже спектр и больше по амплитуде А.

Стоячие волны в помещении[51]. Влияние параллельности стен на акустику помещения заключается в том, что прямоугольная комната представляет собой трехмерный резонатор. В качестве одномерного резонатора можно себе представить узкую трубу, закрытую с двух сторон. Если возле одной из сторон поместить источник синусоидальных колебаний, то вдоль трубы со скоростью звука будет перемещаться синусоидальная звуковая волна, отражаясь от закрытых стенок.

Поместим возле другой стенки трубы микрофон. Изменяя частоту генератора, можно заметить, что при изменении частоты амплитуда звука, фиксируемая при помощи микрофона, то нарастает, то падает почти до нуля. То есть труба демонстрирует амплитудно-частотную характеристику, по виду напоминающую гребенку, причем каждый ее зубец представляет собой акустический резонанс.

Резонанс образуется, если длина трубы кратна половине длины волны возбуждаемых колебаний. Это явление носит название гребенчатой фильтрации.

Прямоугольное помещение с физической точки зрения ведет себя точно так же, как закрытая с двух сторон труба. Разница лишь в том, что в трубе всего одно (аксиальное) направление распространения звуковых волн, тогда как в прямоугольном помещении их неисчислимое количество, причем во многих из них возникают акустические резонансы. Волны, создающие резонансы, подразделяют на три категории.

К первой категории относятся осевые (аксиальные) волны. Их подразделяют на три класса: продольные, поперечные и вертикальные. Звуковые волны каждого из этих классов отражаются только от двух противоположных стен (или от потолка и пола). Ко второй категории относятся касательные волны, которые распространяются, последовательно отражаясь от четырех стен. Последняя категория – так называемые косые волны, отражающиеся последовательно от всех шести ограждающих поверхностей.

Очевидно, что бороться с самим фактом возникновения резонансов в помещении тяжело, а зачастую и не нужно – если резонансы расположены в заданной полосе частот близко друг к другу и равномерно, то форма сигнала в этой полосе частот передается практически без искажений.

Физик-теоретик Филипп Морз вывел формулу для подсчета количества резонансных частот в заданном диапазоне частот в зависимости от объема и линейных размеров помещения [44], откуда видно, что количество резонансов помещения, приходящихся на одну и ту же полосу частот, с понижением частоты существенно уменьшается. Морз подсчитал, сколько в помещении должно быть резонансов в заданном интервале частот для того, чтобы без заметных искажений нести форму звука длительностью порядка 0,1 с. Результат его расчетов таков: в интервале Δf=10 Гц должно быть не менее 10 резонансов.

Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.

Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.

Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x 1 = L (рис. 31). В струне создано натяжение T.

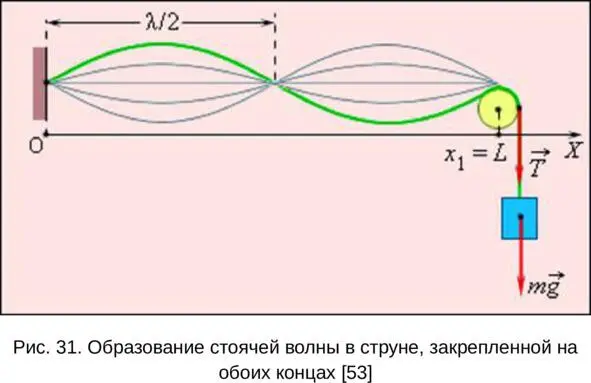
Рис. 31.

По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:

y 1 (x, t) = A cos (ωt + kx) – волна, бегущая справа налево;

y 2 (x, t) = —A cos (ωt – kx) – волна, бегущая слева направо.

В точке x = 0 (один из закрепленных концов струны) падающая волна y 1в результате отражения порождает волну y 2. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции, который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами y 1и y 2в отдельности. Следовательно,

Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.