Николай Кузанский - Об учёном незнании (De docta ignorantia)

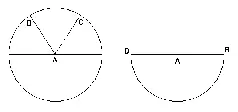
Опять-таки, если В будет обведено вокруг неподвижного A до точки, противоположной своему начальному положению, то есть до D, то из линий AB и AD образуется одна непрерывная линия и будет описан полукруг. Наконец, если этот полукруг будет обведен вокруг неподвижного диаметра BD , то получится шар. И этот шар – последняя возможность линии, целиком переходящей в нем в действительность, потому что шар уже не заключает в себе возможности никакой последующей фигуры.

Поскольку, таким образом, в возможности конечной линии заключены все эти фигуры, а бесконечная линия есть действительным образом все то, возможность чего представляет конечная, то, следовательно, бесконечная линия есть и треугольник, и круг, и шар, что и следовало доказать.

Так как ты, наверное, захочешь яснее убедиться, что бесконечное есть действительность всего, что заключено в возможности конечного, дам тебе совершенно удостовериться в этом.

Воображение, неспособное выйти за пределы чувственных вещей, не улавливает, что линия может быть треугольником, потому что количественное различие обоих несоизмеримо; но для разума это нетрудно.

В самом деле, уже доказано, что максимальным и бесконечным может быть только одно. Ясно также, раз всякие две стороны любого треугольника в сумме не могут быть меньше третьей, что если у треугольника одна из сторон бесконечна, две другие будут не меньше. Потом, поскольку любая часть бесконечности бесконечна, у треугольника с одной бесконечной стороной другие тоже обязательно будут бесконечными. Но нескольких бесконечностей не бывает, и за пределами воображения ты трансцендентно понимаешь, что бесконечный треугольник не может состоять из нескольких линий, хоть этот максимальный, не составной и простейший треугольник есть истиннейший треугольник, обязательно имеющий три линии, и, значит, единственная бесконечная линия с необходимостью оказывается в нем тремя, а три – одной, простейшей. То же в отношении углов: в нем будет только один бесконечный угол, и этот угол – три угла, а три угла – один. Не будет этот максимальный треугольник и состоять из сторон и углов, но бесконечная линия и угол в нем – одно и то же, так что линия есть и угол, раз весь треугольник – линия.

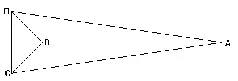
Понять это тебе поможет еще восхождение от количественного треугольника к не-количественному (non-quantum). Всякий количественный треугольник, как известно, имеет три угла, равные двум прямым, и чем больше один угол, тем меньше другие. Хотя каждый угол треугольника может увеличиваться только до двух прямых исключительно, а не максимально, в соответствии с нашим первым принципом, однако допустим, что он увеличивается максимально до двух прямых включительно, оставаясь при этом треугольником. Toгда окажется, что у треугольника один угол, который есть три, и три образуют один. Точно так же ты сможешь убедиться, что треугольник есть линия. Любые две стороны количественного тpeyгольника в сумме настолько длиннее третьей, насколько образуемый ими угол меньше двух прямых; например, поскольку угол BAC много меньше двух прямых, линии BA и AC в сумме много длиннее BC . Значит, чем больше этот угол, например угол BDC , тем меньше линии BD и DC превышают линию BC и тем меньше поверхность. Если допустить, что этот угол приравняется двум прямым, весь треугольник разрешится в простую линию. Таким допущением, у количественных треугольников невозможным, пользуйся для восхождения к не-количественным, у которых, как видишь, невозможное для количественных становится совершенно необходимым. Отсюда тоже ясно, что бесконечная линия есть максимальный треугольник, как и требовалось доказать.

Теперь покажем яснее, что треугольник есть круг. Допустим, что треугольник ABC образован вращением линии AB вокруг неподвижного A до совпадения B с C . Нет никакого сомнения, что если бы линия AB была бесконечной и В описало полный круг, вернувшись к началу, то получился бы максимальный круг, частью которого является BC . Но поскольку BC есть часть бесконечной дуги, BC есть прямая линия; а так как всякая часть бесконечности бесконечна, то BC не меньше всей дуги бесконечной окружности. Таким образом BC будет не только частью, но и совершенно всей окружностью, и, значит, треугольник ABC с необходимостью есть максимальный круг. Причем окружность BC как прямая линия не длиннее бесконечной AB , раз больше бесконечности ничего не может быть; не будут BC и AB и двумя [отдельными] линиями, потому что не может быть двух бесконечностей. Стало быть, бесконечная линия, являясь треугольником, есть также круг, что и надо было установить.

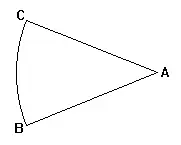
Наконец, что бесконечная линия есть шар, обнаруживается так. Линия AB есть окружность максимального круга и, больше того, сама круг, как уже доказано. Согласно вышеизложенному, она проведена в треугольнике от B до C . Но BC – бесконечная линия, как тоже только что доказано; поэтому AB возвращается в C , совершая полный оборот вокруг себя самой. Когда это происходит, из обращения круга вокруг себя с необходимостью возникает шар.

Итак, если выше доказано, что ABC есть круг, треугольник и линия, то теперь мы доказали, что ABC есть также шар. Это мы и ставили целью разыскания.

Теперь, зная, что бесконечная линия в своей бесконечности есть действительным образом все то, что заключено в возможности конечной линии, мы можем в переносном смысле говорить о простом максимуме, что он есть максимальным образом все то, что заключено в возможности абсолютной простоты: все, что только возможно, то этот максимум есть в максимальной действительности и не как осуществление возможности, а как максимальное бытие; так при получении треугольника из бесконечной линии эта линия есть треугольник не в смысле его построения из конечной линии, а в действительности такая линия уже и есть бесконечный треугольник, представляющий одно и то же с линией. Кроме того, даже абсолютная возможность в максимуме есть не иное что, как сама действительность максимума; так бесконечная линия есть в своей действительности шар. Иначе в не-максимуме: там возможность не есть действительность; так конечная линия не есть треугольник.