Али Альмоссави - Хакни рутину. Как алгоритмы помогают справляться с беспорядком, не тупить в супермаркете и жить проще

Есть ли в нашей повседневной жизни вещи, которые работают как стеки? Как насчет Всемирной паутины? Каждый раз, когда вы кликаете по ссылке, вы помещаете данный сайт в стек. Заходя на эту ссылку еще раз, вы берете веб-адрес из стека. Вам все равно, сколько сайтов вы посетили, пока вы можете вернуться к последнему и от него к другому, стоящему раньше, и так далее.

Можно надеяться, что Ян сумеет разобраться в своем стеке, чтобы внести поправки в манеру общения с почтальоном, и научится лучше определять, когда ему идти за продуктами.

Как-то раз один портной, грек по имени Иоаннис, заблудился в собственной мастерской. Мастерская пользовалась большой популярностью среди афинян, а сам Иоаннис имел репутацию скряги и скопидома. Ситуация осложнялась тем, что помещение располагалось на обширном участке земли, постепенно занимая его, по мере того как Иоаннис в течение 30 лет строил новые проходы и ставил стеллажи для удовлетворения своей страсти к накопительству. И вот он попался: сидит в созданном им же самим лабиринте, заваленном хламом, а вокруг выстроились полки с бесконечными рядами ниток, одежды и разломанных швейных машин. Как же Иоаннису найти путь обратно? Или ему суждено погибнуть здесь?

Есть еще одна греческая история. Когда родился Минотавр, полубык-получеловек, великий архитектор Дедал построил лабиринт, куда было заточено это злое и коварное существо.

«Оказавшись внутри, он бродил по извилистым тропинкам, но так никогда и не нашел выхода. В это место периодически отправлялись молодые афиняне, которых отдавали на съедение Минотавру. И не было у них никакой возможности спастись».

К счастью для Тесея, который тоже должен был стать жертвой Минотавра, дочь царя Ариадна влюбилась в него и разработала план его побега.

Она послала за Дедалом и велела ему показать выход из лабиринта. Тесею она обещала спасение, если он возьмет ее в Афины и там женится на ней. Ариадна дала ему ключ, полученный от Дедала, и клубок пряжи, который Тесей должен был прикрепить к двери и разматывать нить по мере продвижения. Так он и сделал и, конечно же, когда понадобилось, смог проделать путь в обратном направлении. Он смело прошел по лабиринту, нашел Минотавра спящим, убил его и вышел наружу».

Запомните эту историю. Мы скоро вернемся к ней снова. А пока давайте опишем три метода, которые Иоаннис мог бы использовать, чтобы найти выход из мастерской.

ЦЕЛЬ:ВЕРНУТЬСЯ К ВЫХОДУ

МЕТОД 1:ИДТИ ПО ПРОХОДАМ. СВОРАЧИВАТЬ НАУГАД, ПОКА НЕ НАЙДЕШЬ ВЫХОД.

МЕТОД 2:ДЕРЖАСЬ ПРАВОЙ РУКОЙ ЗА СТЕНУ, ИДТИ ВДОЛЬ НЕЕ, СВОРАЧИВАЯ КАЖДЫЙ РАЗ ТОЛЬКО НАПРАВО.

МЕТОД 3:ВЗЯТЬ С ПОЛКИ КАТУШКУ С НИТКАМИ И РАЗМАТЫВАТЬ ЕЕ ПО МЕРЕ ДВИЖЕНИЯ ПО ПРОХОДУ. ЕСЛИ ПОПАДЕШЬ В ТУПИК ИЛИ НАТКНЕШЬСЯ НА СВОЮ ЖЕ НИТКУ, ТО ПОВЕРНУТЬ НАЗАД И ПОЙТИ ПО ДРУГОМУ ПРОХОДУ.

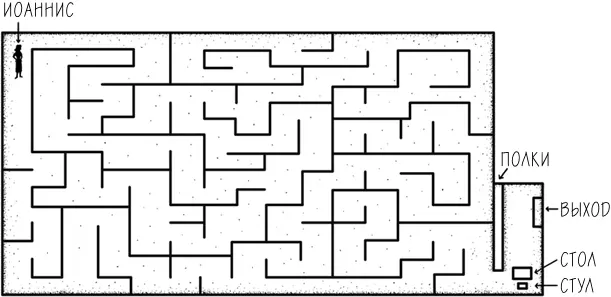
Метод 1 имитирует путь мыши в лабиринте. Никаких продвинутых умственных способностей для него не требуется – просто беспорядочное хождение от одной точки до другой, пока по случайности не наткнешься на кусок сыра. Иногда его так и называют – метод беспорядочной мыши. Как вы можете догадаться, результат достигается крайне медленно.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Ричард Фейнманн (1918–1988) – американский физик-теоретик; Джон фон Нейман (1903–1957) – венгерский и американский математик; Чарльз Дарвин (1809–1888) – автор теории эволюции (прим. ред.).

Все линии изображены на графике двойного логарифмического масштаба, поэтому они имеют такой вид ( прим. автора ).

Важно в самом начале отметить, что эти характеристики не всегда применимы к другим сферам жизни, например к учебе, где скорость – не главное. По моему опыту та обучающая среда, которая требует от студентов работать быстро, настраивает их на неудачу ( прим. автора ).

В этой книге есть смешной отрывок об Оливере Хивсайде, остром на язык отшельнике, чей подход к математике проектирования отличался особой прагматичностью. Инженеры хвалили метод Хивсайда, но математики смеялись над ним из-за недостатка точности. У Хивсайда же не было времени проявлять дотошность («Стоит ли мне отказываться от ужина, если я не понимаю, как происходит пищеварение?»). ( Прим. автора .)

Фрэнсис Бэкон (1561–1626) – один из крупнейших философов Нового времени, основоположник эмпиризма и английского материализма ( прим. ред .).

«Помни» («Memento») – фильм Джонатана Нолана (2000). Главный герой, переживший тяжелую травму головы, не может ничего удержать в памяти больше 15 минут.

Факт, который часто описывают фразой «торговать памятью за деньги» ( прим. автора ).

Этот подход был впервые применен в Университете Торонто десять лет назад, и сейчас его называют глубоким обучением ( прим. автора ).

Заметьте, что, применяя оба метода, мы не занимаемся отделением носков от не-носков, поскольку наше задание – разобраться только с носками ( прим. автора ).

Есть более сложные методы изучения скорости роста. Один из них – узнать, не растет ли определенный метод быстрее, чем показанная скорость (известная под названием большое-о), или медленнее, чем показанная скорость (известная как большое-Ώ, т. е. «большая омега»). Другой метод – посмотреть, описывают ли скорости роста лучшие, худшие или средние случаи. Мы поговорим обо всех этих случаях позже ( прим. автора ).

В этом примере Марджи не особенно заботится о том, в каком порядке лежат неразобранные носки. Все, что ее беспокоит, – все носки должны быть отложены в одну сторону.

Например, найти сумму первых чисел n было бы сложно, если бы вы проходились по этим n-числам один за другим, каждый раз суммируя пары. Гораздо удобнее использовать вместо этого формулу n x (n+1)/2 ( прим. автора ).