Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Всего получается 156 циклов. Из них пустых 156 – 14 = 142. Соответственно, за каждый из оставшихся 14 циклов собирается один клаттер. Заходить на второй виток ни разу не приходилось. Сеть проходит четыре гармонические стадии роста: в момент старта, а также на 93-м, 134-м и 156-м цикле с числом клаттеров 2, 4, 8 и 16, соответственно. Переходим ко второму этапу.

Рис. 2. Алгоритм роста сети 256 от 16-ти до 256-ти клаттеров.

На этом этапе пройдено 15 циклов. Его начало сопровождается бурным ростом числа клаттеров. Это связано с тем, что на втором этапе за цикл с нуля собирается один или большее число клаттеров. Для реализации прохода через гармонические сети необходимо было скорректировать рост, но только в четырех точках «близких» к гармоническим сетям.

Каждая коррекция представляла собой малое возмущение в один клаттер и была проведена на стадиях роста с числом клаттеров 20, 31, 65 и 127: (127 + 1)*2 = 256, (31 + 1)*8 = 256, (65-1)*4 = 256. Существует не одна такая четверка, но результат, функция U(C), – остается тем же.

Растущая сеть проходит через гармонические стадии с размером: 16, 32, 64, 128, 256 клаттеров. На последнем цикле число клаттеров удваивается: U(14) = 128, U(15) = 256. Это справедливо для сетей любого ранга. Отметим также, что результаты работы алгоритма практически полностью совпадают со значениями следующей функции:

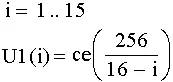
Рис. 3. Теоретическая гипербола сети 256.

Назовем функцию U1(i) теоретической гиперболой сети 256.Этап заканчивается сборкой клаттера 65536. И, наконец, третий этап роста сети 256 – репликация. Здесь сеть собирает свою копию и прокладывает связь между ней и оригиналом. Сеть 65536 может стартовать.

Подведем итоги для сети 256: всего имеется 156 + 15 = 171 цикл (без учета репликации) и восемь гармонических стадий роста с числом клаттеров 2, 4, 8, 16, 32, 64, 128, 256. Последняя гармоническая сеть с числом клаттеров 256 является также совершенной.

Продолжая процесс, переходим к сети 65536. Первый этап – рост от 2-х клаттеров до 256-ти.

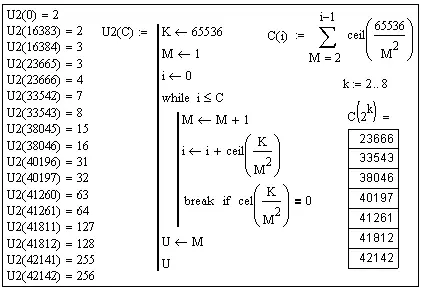
Рис. 1. Рост сети 65536 от 2-х клаттеров до 256-ти.

Всего сеть проходит 42142 цикла. Из них пустых 42142 – 254 = 41888. В 254 циклах собиралось по одному клаттеру. На второй виток, в соответствии с алгоритмом, заходить не приходилось.

Имеется восемь гармонических стадий роста: на старте и на 23666-м, 33543-м, 38046-м, 40197-м, 41261-м, 41812-м, 42142-м циклах с числом 2, 4, 8, 16, 32, 64, 128 и 256 клаттеров, соответственно.

Второй этап – рост от 256-ти клаттеров до 65536-ти.

Рис. 2. Рост сети 65536 от 256-ти клаттеров до 65536-ти.

Коррекция роста проведена в 21 точке. Все значения размеров сети, для которых проводилась коррекция М <���− М+1, являются (или «почти» являются) делителями числа 65536, если к ним добавить единицу; например, 65536/(13106+1) = 5,000076. Вот частные, которые получаются в результате:

3, 4, 5, 8, 19, 32, 56, 67, 94, 122, 212, 214, 217, 222, 225, 229, 234, 240.

Такие коррекции одни из многих возможных, подобных им, но все они дают практически один и тот же результат, если придерживаться правила: при небольшом отклонении от гиперболической сети добавить в цикл один клаттер, т. е. держать курс на ближайшую гиперболическую сеть. Гиперболическая сеть – это сеть, размер которой равен ce(65536/N), где N > 256 – натуральное число.

Причем при увеличении М на единицу процесс устойчив и через некоторое количество циклов «садится» на гиперболу. При уменьшении М на единицу наблюдается неустойчивость, и процесс роста необратимо уходит от гармонических сетей.

Понадобилась одна коррекция в сторону уменьшения размера сети М: 328 <���− 327 (65536/328 = 199.8), если ее не провести процесс срывается с гиперболы (последние три цикла 25501, 43735, 65537). Результаты работы алгоритма «почти точно» ложатся на теоретическую гиперболу сети 65536:

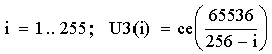
Рис. 3. Теоретическая гипербола сети 65536.

Гиперболический рост сети на первом и втором этапе представляет собой ускоряющийся неустойчивый процесс, требующий от управляющей системы двадцать пять коррекций. Неустойчивость роста понятна и из того факта, что уравнение Капицы, как асимптотический закон роста сети, устойчивых решений не имеет.

Составим таблицу зависимости числа клаттеров растущей сети от номера цикла для алгоритма и теоретической гиперболы. Значения почти совпадают: максимальное отличие в три клаттера. В таблице выделены гармонические размеры сети.

Таблица 1. Зависимость числа клаттеров растущей сети от номера цикла для алгоритма и теоретической гиперболы.

Третий этап – операция репликации. Собираются копия сети, прокладывается связь между ней и оригиналом. Сеть 4 294 967 296 может стартовать.

Всего имеется 42142 + 255 = 42397 циклов (без учета репликации) и 16 гармонических стадий роста сети 65536. Сведем все данные в таблицы:

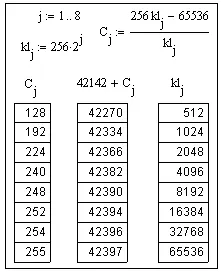
Таблица 2А. Подсчет номера цикла и числа клаттеров для гармонических сетей с размером, принадлежащем интервалу [257, 65536].

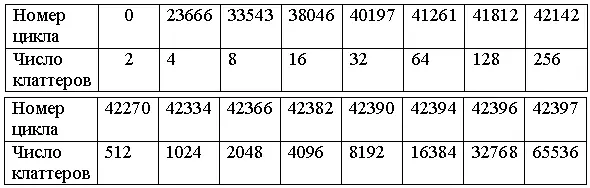
Таблица 2В. Зависимость числа клаттеров от номера цикла для гармонических размеров сети 65536.

Для того, чтобы найти полное количество циклов, которое проходит сеть любого ранга в процессе своей эволюции, нужно сложить число этих циклов на трех этапах ее роста (считаем, что сеть любого ранга, став совершенной, создает единственную свою копию, на что уходит ровно два цикла [8]и рост сети следующего ранга всегда начинается с двух клаттеров.)

На втором и третьем этапе число циклов вычисляется с полной определенностью: корень квадратный из веса клаттера минус единица плюс два. Минус единица, т. к. алгоритм восьми шагов прекращает свою работу за шаг до сингулярности. И далее два цикла на переход. Получаем корень квадратный из веса клаттера плюс единица.