Анатолий Молчанов - Население Земли как растущая иерархическая сеть

В первой части, сингулярность Дьяконова – Капицы будет определена нами исходя из развиваемой здесь гипотезы о растущей сети, сопровождающей эволюционный и исторический процесс. Такое определение, разумеется, не может быть бесспорным, поскольку опирается на гипотезу.

Так как ошибка здесь недопустима по этическим соображениям, ведь эта историческая сингулярность ассоциируется с именами известного историка и выдающегося популяризатора науки, – нами будет еще раз дано ее определение, но уже без всяких ссылок на нашу гипотезу, а на основании лишь известных исторических фактов. Это будет сделано во второй части нашей работы.

Прежде всего, покажем, что сингулярность Дьяконова – Капицы, согласно предлагаемой здесь гипотезе, приходится на 2022 год с погрешностью примерно в два, три года и в полном соответствии с демографическими данными. Запишем формулу теоретической гиперболы:

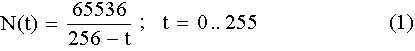
Рис. 1. Зависимость числа носителей сети в клаттерах от неолита до второй половины ХХ века.

Здесь N(t) – численность носителей в клаттерах (один клаттер содержит 65536 носителей), а t – время в циклах τ (τ = 40 лет) от начала неолита. Моменты времени t = 0, 128, 192, 224, 240, 248, 252, 254, 255 – даты, когда сеть достигает гармонической стадии своего роста. (Продолжительность восьми исторических периодов, соответственно: 128τ, 64τ, 32τ, 16τ, 8τ, 4τ, 2τ, т.) Момент t = 256 – точка сингулярности или время окончания первого цикла демографического перехода, если отсчет времени вести от начала неолита.

Если отсчет вести от начала новой эры, точку сингулярности получаем, прибавляя к дате достижения сетью совершенства (т. е. к 1982 году) время цикла сети: 1982 + 40 = 2022. Постоянная Форстера для теоретической гиперболы равна: С = kK 2τ = 1.1*65536 2*40= 1.89*10 11лет. Если к тому же время измерять в годах, а численность в миллиардах человек, то формула (1) приобретает вид:

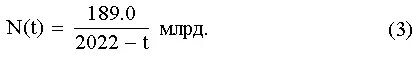
Рис. 2. Зависимость численности населения Земли от неолита до наших дней согласно теории.

Но именно так и выглядит эмпирическая гипербола, лучше всего описывающая рост населения мира за последние сорок тысяч лет:

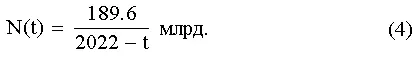
Рис. 3. Зависимость численности населения Земли от палеолита до наших дней по данным Мак-Эведи, Джоунса и Кремера.

Эта гиперболическая зависимость, из семейства гипербол Форстера, лучше всего задает рост численности населения мира от 40.000 г. до н. э. до 1970 г. по данным Мак-Эведи, Джоунса (1978) и Кремера (1993) для периода от 40.000 г. до н. э. до 1950 г. н. э., а также по данным Бюро переписей США за 1950–1970 гг. [13]

Зависимость (4) можно получить и из формулы Форстера (см. главу «Константы Капицы»), если подобрать гиперболу с целочисленным показателем n = -1, находящуюся на наименьшем «расстоянии» от гиперболы Форстера с n = -0.99 и C = 179 млрд. У этой гиперболы C = 188 млрд и t 0= 2022, что практически не отличается от данных Мак-Эведи, Джоунса и Кремера.

Теоретическая гипербола (3), а значит и (1), практически тождественна гиперболе (4). Причем эта гиперболическая зависимость описывает с хорошей точностью рост населения мира вплоть до конца семидесятых, начала восьмидесятых годов прошлого столетия. Это вытекает из того простого факта, что теоретическая гипербола по определению должна проходить через точку (1982; 65536 2); учитывая то, что сеть достигает совершенства в 1982 году, а зомби-коэффициент k = 1.1, получаем: 1,89*10 11/[(2022–1982)*1.1] ≈ 65536 2. Следовательно, 2022 год – дата, отстоящая от момента завершения роста сети на время цикла сети – действительно, точка сингулярности.

Построим в одних координатных осях гиперболу (4) и график интерполяции данных по численности населения мира в интервале: 1960–1990 гг. по данным International Data Base (IDB) с шагом в один год.

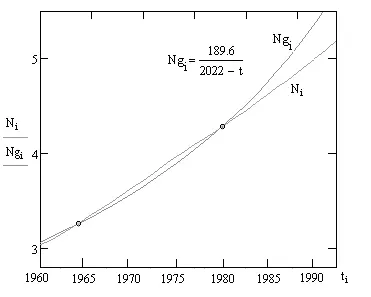
Рис. 4. Гипербола (4) и интерполяция демографических данных за 1960–1990 гг.

Последнее максимальное сближение, а фактически пересечение эмпирической и совпадающей с ней теоретической гиперболы (4) с графиком интерполяции демографических данных произошло в конце семидесятых, начале восьмидесятых годов прошлого столетия, а затем эти кривые разошлись навсегда. Поэтому именно 1982 год (с погрешностью в 2–3 года) можно с достаточным основанием считать моментом окончания гиперболического роста и началом первого цикла демографического перехода.

Согласно феноменологической теории Капицы, демографический переход начался в шестидесятых годах двадцатого столетия (в 1965 году), когда скорость роста населения мира достигла своего абсолютного максимума 2 % в год и затем начала убывать. Такое представление противоречит предлагаемой здесь гипотезе. Действительно, хотя скорость роста и достигает своего максимума в 1965 году, а затем уменьшается, однако кривая роста на рис. 4 с этого момента начинает опережать гиперболу Форстера.

А поскольку идеальную гиперболу (4) c ее точкой сингулярности в 2022 году «обогнать» невозможно, фактическая (без сингулярности) кривая роста должна ее где-то до этой точки пересечь. То, что кривые пересекаются при t = 1982, т. е. в тот момент времени, когда сеть становится совершенной, говорит о том, что в соответствии с предлагаемой здесь теорией «расставание» роста с гиперболой и начало глобального демографического перехода приходятся на конец семидесятых, начало восьмидесятых, а не на середину шестидесятых годов двадцатого столетия, как полагал С.П. Капица.

Следовательно, теория полностью соответствует демографическим данным. Причем 1982 год с точностью до одного, максимум трех лет и есть тот момент времени, когда сеть достигает совершенства, а 2022 год (1982 + 40 = 2022), соответственно, – конец первого цикла демографического перехода или точка сингулярности теоретической (и эмпирической) гиперболы демографического роста.

Согласно предлагаемой здесь теории на кривой роста численности населения Земли имеется пять особых точек:

1,7 млн лет назад– старт роста сети человека, начало эволюции Homo sapiens.

8 тыс. лет до н. э.– переход ко второму этапу роста сети; начало неолита и взрывного демографического роста.

1982 год– сеть достигает совершенства, эволюция человека заканчивается.

2022 год– окончание первого цикла демографического перехода; сингулярность Дьяконова – Капицы.