Анатолий Молчанов - Население Земли как растущая иерархическая сеть

И, во-вторых,во второй половине двадцатого столетия начался глобальный демографический переход: явление, хорошо изученное для отдельных, прошедших свой «локальный» переход стран. Переход, истинная причина которого – называются десятки причин – до сих пор остается непонятной и даже загадочной. Несомненно только то, что является он глобальным, т. е. это согласованный для всех стран и народов процесс; происходит он в XX – XXI вв. и численность населения Земли после него стабилизируется и расти больше не будет.

Существуют различные прогнозы роста численности человечества на ближайшие сто и двести лет. Любой не катастрофический прогноз предполагает ее стабилизацию на некотором фиксированном уровне, определяемом ресурсами и экологией. Наиболее логичной представляется стабилизация, происходящая сразу после перехода, поскольку численность населения ряда стран Европы и Америки, уже прошедших свой «локальный» демографический переход, больше не растет и (в первом приближении) не уменьшается. Несомненно также и то, что явление это не только демографическое, но также социальное и историческое.

Итак, существуют две важнейшие даты мировой истории: момент начала неолита (и начала взрывного гипеболического роста), когда по всей Ойкумене происходит, причем по историческим меркам мгновенно, переход от охоты и собирательства к скотоводству и земледелию.

И точка сингулярности эмпирической гиперболы демографического роста, определяющая момент окончания длившегося тысячелетиями гиперболического роста населения Земли и время прохождения глобального демографического перехода. Назовем эту демографическую и историческую сингулярность сингулярностью Дьяконова – Капицы.

Отметим также, что обе эти даты – реальные исторические вехи, не связанные ни с какими теориями. За момент начала неолита берем 8154 год до н. э., время Т 0положим равным 2022 году; постоянную Форстера примем равной 189,6*10 9лет.

Для дальнейшего нам понадобятся некоторые сведения из элементарной математики. Гипербола y = 1/x обладает тем очевидным свойством, что при уменьшении аргумента в два раза, ее значение возрастает в два раза. Геометрическая прогрессия со знаменателем 1/2 обладает одной особенностью, выделяющей ее среди других прогрессий.

Она заключается в том, что каждый последующий ее член, будучи отмечен точкой на числовой оси, есть середина отрезка, соединяющего точку, изображающую предыдущий член и точку, представляющую предел общего члена прогрессии (точку нуль).

Иначе говоря, члены этой прогрессии можно отметить последовательностью шагов по числовой оси, в которой каждый последующий шаг вдвое короче предыдущего. Пусть теперь аргументами гиперболы будут члены геометрической прогрессии, с первым членом равным единице и знаменателем 1/2:

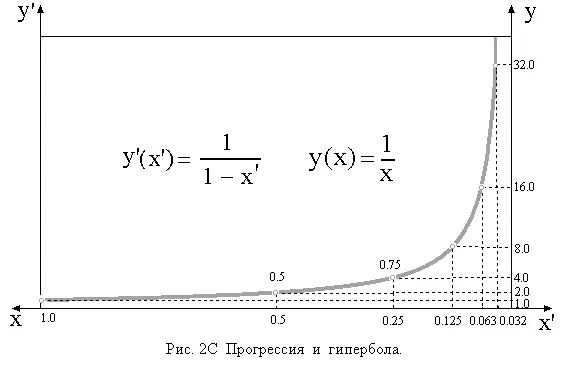
Рис. 2. Прогрессия и гипербола.

Тогда последовательность значений аргумента будет составлять бесконечно убывающую прогрессию со знаменателем 1/2, а последовательность значений функции, соответственно, – бесконечно возрастающую прогрессию со знаменателем равным двойке. Произведение x*y будет постоянным и равным единице. Построим график y(x) = 1/x (ось 0X направим влево, ось 0Y – вверх).

Если перейти к системе координат с началом сдвинутым на единицу в положительном направлении оси 0Х, а саму эту ось обратить (направить вправо), то уравнение гиперболы примет вид: y'(x') = 1/(1-x'). Последовательность точек на числовой оси, которая в исходной системе координат определялась бесконечно убывающей прогрессией, в преобразованной системе задается последовательностью сумм этой прогрессии.

Применим эту математику для разбиения всей истории развития человечества от неолита до наших дней. Формула гиперболы мирового демографического роста имеет вид:

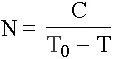
Рис. 1. Гипербола демографического роста населения Земли.

Где Т 0= 2022 + 8154 = 10176 год – дата сингулярности, если время отсчитывать от начала неолита. Составим теперь последовательность времен по следующему правилу, которое назовем алгоритмом восьми шагов:

• Во-первых, все времена будем отсчитывать от момента начала неолита, и первый член этого ряда положим равным нулю;

• Второй член данного ряда – это точка на оси времени, которая делит пополам отрезок времени от начала неолита до сингулярности Дьяконова – Капицы, т. е. 10176/ 2 = 5088;

• Остальные члены определяются последовательностью, состоящей из семи шагов по оси времени, в которой каждый последующий шаг вдвое короче предыдущего.

Предел этой прогрессии: 10176 год (при отсчете времени от начала неолита) – сингулярность Дьяконова – Капицы. Пересчитаем в соответствии с обозначенным здесь алгоритмом границы восьми исторических периодов, взяв за начало отсчета времени нулевой год н. э.

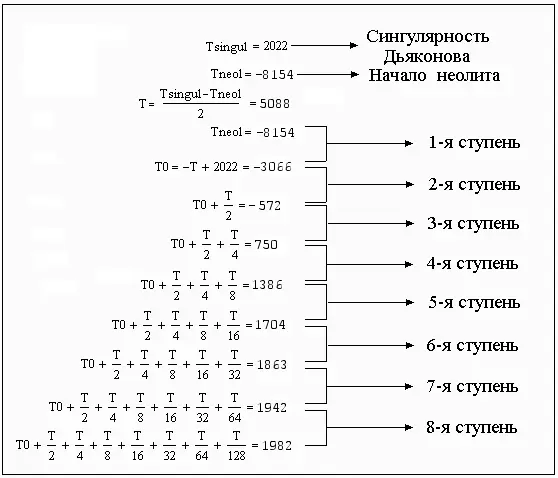
Рис. 3. Восемь ступеней исторического развития. Отсчет времени ведется от начала новой эры.

Таким образом получаем восемь ступеней, периодов или фаз исторического развития. При этом продолжительность каждого последующего периода в два раза меньше предыдущего, численность населения мира за время его развертывания удваивается, а инвариантом процесса является постоянная Форстера.

В качестве показателя исторического изменения при периодизации по алгоритму восьми шагов выступает растущая по гиперболическому закону численность населения Земли.

Казалось бы, в полученных результатах нет ничего особенного – это всего лишь математика. Можно было бы взять любой, достаточно удаленный момент времени в прошлом и 2022 год, рассчитать таким способом восемь исторических периодов, и численность населения также будет удваиваться от периода к периоду. Но оказывается, что лишь тогда, когда алгоритм стартует с момента начала неолита, разметка исторического времени на периоды соответствует действительности.

Следовательно, существуют девять фиксированных, особенных значений переменной «численность населения Земли», при достижении которых и происходят фундаментальные исторические изменения в человеке и обществе. На вопрос: почему это так? – ответа нет. Так же как и на вопрос о том, точные ли даты исторического времени соответствуют таким значениям численности, или алгоритм задает лишь их математические ожидания.