Анатолий Молчанов - Население Земли как растущая иерархическая сеть

9.Для полноты картины можно добавить также и «ненаучный» аргумент в подтверждение уникальности, неповторимости и значимости того краткого момента истории конца семидесятых начала восьмидесятых годов прошлого столетия, о котором идет речь. Ведь именно на это время приходится пик активности НЛО, активности невиданной за всю историю наблюдений этого явления. Нечто подобное было зафиксировано еще только один раз спустя десятилетие в 1990 году.

Ответа на вопрос, что же в действительности произошло в конце семидесятых, начале восьмидесятых годов двадцатого века, в чем причина цикличности развития и гиперболического роста населения Земли применяемая здесь феноменологическая схема не дает. Но можно считать, как было показано нами ранее, что именно в это время (в 1982-м, а не в 1965 году) закончился рост человечества по закону гиперболы и начался демографический переход. И тогда же завершился последний, восьмой исторический период, а вместе с ним и циклический ход мирового исторического процесса.

Казалось бы, не может быть никакой теоретической формулы, описывающей гиперболический рост численности населения мира. А постоянная Форстера и точка сингулярности гиперболы демографического роста – чисто эмпирические константы.

Тем не менее, если квант исторического времени существует, алгоритм восьми шагов отвечает действительности, а в момент окончания гиперболического роста численность носителей сети достигает значения 2 32– такую формулу легко сконструировать:

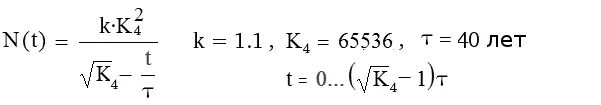
Рис. 1. Теоретическая зависимость численности населения Земли от времени N(t). Отсчет времени ведется от начала неолита; K 4≈ K; K, τ – постоянные Капицы; k – зомби-коэффициент, учитывает долю народонаселения, находящуюся вне Сети.

Длительность исторического цикла τ положим равной сорока годам, отсчет времени ведем от начала неолита. Гиперболический рост занимает 255 циклов; в момент его окончания в 1982 году численность носителей сети достигает значения 2 32, а численность населения Земли, соответственно, – k*2 32= 4,7 млрд и данная формула перестает правильно описывать рост.

Сингулярность теоретической гиперболы, сингулярность Дьяконова – Капицы, наступает в момент времени t = 256τ. Постоянная K 4, определяющая рост, связана с безразмерной константой Капицы К и с постоянной Форстера С следующим образом: K = √k* K 4= 1.05*65536 = 68700, С = k*K 4 2τ = 1.1*65536 2*40 = 1.89*10 11.

Здесь нужно отметить следующее: если алгоритм восьми шагов отвечает действительности, то постоянная K 4в формуле на рис. 1 (приблизительно равная постоянной Капицы К) должна быть в точности равна 65536. Действительно, в соответствии с теорией Капицы, а также согласно нашей теории, произведение корня квадратного из K 4(K) на τ равно продолжительности всего исторического периода развития человека, как его обычно принято определять: от неолита до наших дней. Следовательно, корень из K 4(K) равен числу циклов до сингулярности Дьяконова – Капицы, т. е. 256, а K ≈ K 4= 256 2= 65536. Показатель сжатия исторических периодов в таком случае должен быть равен двум, а не 2.7, как в работах С.П. Капицы.

С.П. Капица в последней своей работе «Парадоксы роста…» 2010 года все таки «пришел к выводу», что показатель сжатия исторических периодов должен быть равен двум (стр. 182). Т. к. за момент начала неолита у него взята дата 9000 лет до н. э., т. е. мало отличается от той, что принята в нашей модели, то не только количество циклов, которых должно быть 15, а не 11, но и разметка исторического времени на эти циклы у него должна быть примерно такой же, как у нас.

На самом деле для коэффициента сжатия исторических периодов он получил величину e/(e – 1) = 0.583, которую странным образом округлил до 0.5, что соответствует показателю сжатия, равному двум (1/0.583 ≈ 1.7 ≈ 2). При этом автор «Парадоксов роста» не счел нужным упомянуть ни работу Ю.В. Яковца 1997 года, в которой этот показатель равен 1.8, что ближе к двойке, чем у него, ни нашу работу 2006 года, в которой он в точности равен двум. С.П. Капица – и это характерно для его творчества – трудности, которые испытывает его теория, – никак не отмечает, своих ошибок – никогда не признает, на предшественников, как правило, – не ссылается.

Постоянная τ – единственная размерная постоянная, определяющая гиперболический рост, есть не что иное как: постоянная времени Капицы, время цикла растущей сети в нашей модели, длительность Кондратьевского цикла, продолжительность последнего, восьмого исторического периода 1942–1982 гг., половина длительности глобального демографического перехода 1982–2062 гг., учетверенная длительность одиннадцатилетнего Солнечного цикла (?). Это фундаментальная постоянная времени, задающая масштаб, в котором должно измеряться историческое время от неолита до наших дней.

Зависимость численности населения Земли от времени в соответствии с предложенной формулой на рис. 1, так же как и показатели продвижения цивилизации по пути исторического развития от начала неолита до 1982 года зависели только от отношения времени t к постоянной τ, т. е. от количества циклов, пройденных Мир-системой к моменту времени t.

Если отсчет времени вести в циклах от сингулярности Дьяконова – Капицы в прошлое, теоретическая гипербола приобретает наиболее простой вид:

Рис. 2. Зависимость численности населения Земли от числа циклов до исторической сингулярности N(T).

Например, чтобы подсчитать сколько людей проживало в 1700 году сначала находим число циклов до сингулярности Дьяконова – Капицы: (2022–1700)/40 = 8,05 цикла. Затем 1,1*4,3 миллиарда делим на 8,05 и получаем 590 миллионов человек.

Средняя длительность инновационных циклов, так же как продолжительность глобальных исторических периодов Мир-системы, выражается через фундаментальную константу исторического времени τ по одной и той же формуле (обобщение гипотезы Й. Шумпетера):

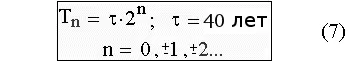
Рис. 3. Длительность экономических и глобальных исторических циклов, выраженная через квант исторического времени τ.

При этом продолжительность сокращающихся по закону прогрессии исторических периодов Дьяконова – Капицы может быть получена, если брать целые неотрицательные значения n в пределах от нуля до семи. Если же брать значения n > 7, то получаются периоды эволюции Homo sapiens, но расположение этих периодов на оси времени не отвечает данным палеоантропологии, т. е. применяемая феноменологическая схема перестает соответствовать действительности.